Contents
Mạng nơ-ron sâu đã tạo ra nhiều đột phá gần đây trong nhiều lĩnh vực như thị giác máy, xử lý ngôn ngữ tự nhiên hay xử lý giọng nói. Tuy nhiên, bất chấp sự phổ biến của mạng nơ-ron, các nhà nghiên cứu vẫn đang cố gắng tìm hiểu các nguyên tắc cơ bản chi phối chúng. Các lý thuyết cổ điển như chiều VC và độ phức tạp Rademacher thường gợi ý rằng các mô hình có quá nhiều tham số (overparameterized) sẽ tổng quát hóa kém trên dữ liệu không nhìn thấy. Tuy nhiên, những công trình gần đây đã phát hiện ra rằng các mô hình quá nhiều tham số như mạng nơ-ron vẫn có khả năng khái quát hóa tốt. Để cải tiến các mô hình này, cần xây dựng một góc nhìn hiện đại hơn để hiểu rõ hơn về tổng quát hóa.
1. Khái niệm tổng quát hóa
Để đánh giá một mô hình học máy, khả năng học trên tập huấn luyện không phải là tiêu chí tiên quyết. Người ta thường quan tâm hơn tới việc mô hình sau khi huấn luyện sẽ thể hiện thế nào trên tập dữ liệu chưa nhìn thấy, tức là khả năng tổng quát hóa (generalization) của nó.
Xét $\mathcal{D}$ là một phân phối trên tích đề-các $\mathcal{X} \times \mathcal{Y}$ với $\mathcal{X}$ là không gian dữ liệu đầu vào nào đó (ví dụ tập các hình ảnh) và $\mathcal{Y}$ là không gian đầu ra tương ứng (ví dụ tập nhãn phân loại các ảnh). Xét mô hình $f : \mathcal{X} \rightarrow \mathcal{Y}$ và tập huấn luyện $\Omega = \{(x_i, y_i), i = 1, 2, \ldots, n\}$, trong đó các điểm dữ liệu $(x_i, y_i)$ được lấy mẫu độc lập và tuân theo phân phối giống nhau (i.i.d.) từ phân phối $\mathcal{D}$. Quá trình huấn luyện $f$ thường được quy về bài toán cực tiểu hóa hàm rủi ro thực nghiệm:
$$\hat{R}_{n}(f) \triangleq \frac{1}{n}\sum_{i=1}^{n}L(f(x_i),y_i) \tag{1} \label{eq1}$$
trong đó $L(f(x_i),y_i)$ là hàm chi phí được định nghĩa trước.
Tuy nhiên, hiệu năng của mô hình phải được đánh giá trên toàn bộ phân phối dữ liệu $\mathcal{D}$, bao gồm cả những dữ liệu chưa nhìn thấy (dữ liệu test), sử dụng độ đo gọi là rủi ro kỳ vọng:
$$R(f) \triangleq \mathbb{E}_{(x,y) \sim \mathcal{D}}[L(f(x),y)] \tag{2} \label{eq2} $$
Khoảng cách tổng quát hóa (generalization gap) hay còn gọi là sai số tổng quát hóa (generalization error) của mô hình $f$ được định nghĩa như sau:
$$ \Delta R(f) \triangleq R(f) – \hat{R}_{n}(f) \tag{3} \label{eq3} $$
Lý tưởng nhất là tìm ra được mô hình tối ưu $f^*$ cực tiểu hóa rủi ro kỳ vọng:
$$R^* \triangleq R(f^*)=\inf\limits_{f : \mathcal{X} \rightarrow \mathcal{Y}} R(f) \tag{4} \label{eq4}$$
$$f^* \triangleq \underset{f : \mathcal{X} \rightarrow \mathcal{Y}}{\arg\min} R(f)$$
$R^*$ gọi là rủi ro Bayes. Trong thực tế ta không thể giải bài toán ($\ref{eq4}$) trên toàn bộ không gian mô hình $\{f : \mathcal{X} \rightarrow \mathcal{Y} \}$. Thương thường, người ta sẽ mô hình hóa bài toán bằng một họ mô hình $\mathcal{F}$ (ví dụ một kiến trúc mạng nơ-ron, một bộ phân lớp SVM…) và cố gắng tìm ra mô hình tối ưu nhất $f^*_{\mathcal{F}}$ trong họ $\mathcal{F}$ để cực tiểu hóa rủi ro kỳ vọng:
$$R^*_{\mathcal{F}} \triangleq R(f^*_{\mathcal{F}})=\inf\limits_{f \in {\mathcal{F}}} R(f) \tag{5} \label{eq5}$$
$$f^*_{\mathcal{F}} \triangleq \underset{f \in {\mathcal{F}}}{\arg\min} R(f)$$
Vì thực tế không thể có toàn bộ dữ liệu từ phân phối $\mathcal{D}$ để giải bài toán ($\ref{eq5}$) nên ta phải học trên tập dữ liệu huấn luyện $\Omega$ nào đó được lấy mẫu từ $\mathcal{D}$. Do đó, bản chất quá trình học là tìm mô hình (bộ tham số) tối ưu nhất $f^*_n$ trong họ $\mathcal{F}$ cực tiểu hóa rủi ro thực nghiệm (ERM – emperical risk minimization):
$$\hat{R}^*_{\mathcal{n,F}} = \hat{R}(f^*_n) \triangleq \inf\limits_{f \in {\mathcal{F}}} \hat{R}_{n}(f) = \inf\limits_{f \in {\mathcal{F}}} \frac{1}{n}\sum_{i=1}^{n}L(f(x_i),y_i) \tag{6} \label{eq6}$$
$$f^*_n \triangleq \underset{f \in {\mathcal{F}}}{\arg\min} \hat{R}_n(f) $$
Mục tiêu lý tưởng (ultimate goal) của học máy là tìm học được mô hình $f^*_n$ có rủi ro kỳ vọng đúng bằng rủi ro Bayes:
$$ R(f^*_n)~-~ R^* = 0 \tag{7}\label{eq7}$$
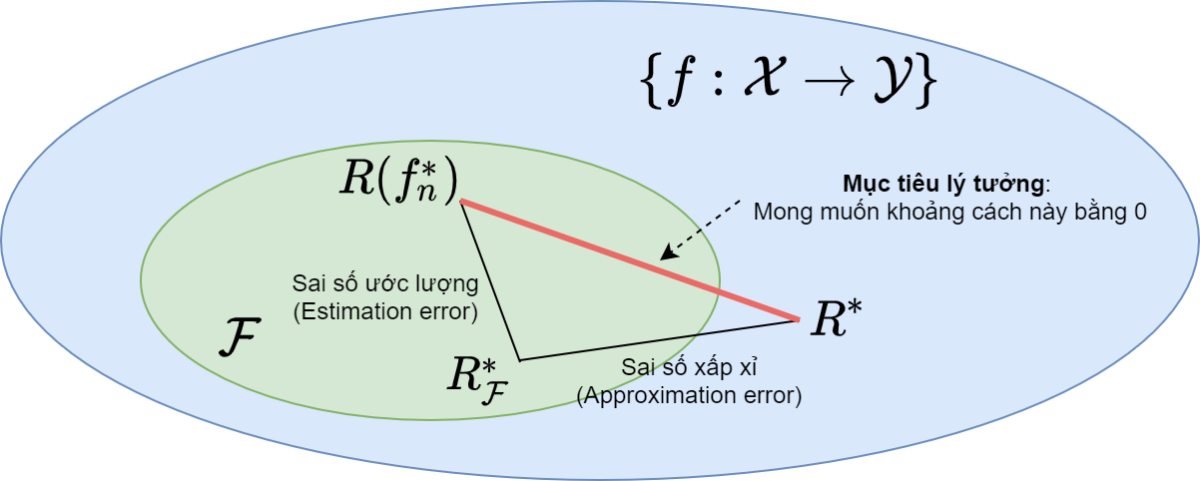
Bức tranh toàn cảnh thể hiện trên Hình 1. Để hướng tới mục tiêu trong Công thức (\ref{eq7}), ta cần quan tâm hai sai số thành phần: sai số ước lượng và sai số xấp xỉ:
$$ R(f^*_n) ~-~ R^* = \underbrace{R(f^*_n)~- ~R^*_{\mathcal{F}}}_{Sai~số~ước~lượng} + \underbrace{R^*_{\mathcal{F}} ~-~ R^* }_{Sai~số~xấp~xỉ}\tag{8}$$
Trong khi sai số xấp xỉ bị chi phối bởi cách mô hình hóa bài toán, sai số ước lượng là một tính chất của quá trình học, quyết định mô hình học hiệu quả hay không.
Do đó mục tiêu của quá trình học là cho trước một họ mô hình $\mathcal{F}$, cần học ra mô hình $f^*_n \in \mathcal{F}$ để cực tiểu hóa sai số ước lượng:
$$R(f^*_n) ~- ~R^*_{\mathcal{F}} \leftarrow \min \tag{9} \label{eq9}$$
2. Đánh giá độ phức tạp của họ mô hình
2.1. Hệ số phá vỡ và số chiều VC
Xét trường hợp phân loại nhị phân $\mathcal{Y} = \{0, 1\}$. Hệ số phá vỡ tập dữ liệu $\mathbf{X} = \{x_1, x_2, \ldots, x_n\}$ của họ mô hình $\mathcal{F}$, ký hiệu là $S_{\mathcal{F}}(\mathbf{X})$, thể hiện số lượng hành vi khác nhau mà họ mô hình $\mathcal{F}$ tác động lên tập dữ liệu :
$$ S_{\mathcal{F}}(\mathbf{X}) \triangleq |\{f(\mathbf{X}) : f \in \mathcal{F}\}| \tag{10} \label{eq10}$$
trong đó $f(\mathbf{X}) = [f(x_1), f(x_2),\ldots,f(x_n)]$ là tập các dự đoán của mô hình $f$ trên tập dữ liệu $\mathbf{X}$.
Với phân lớp nhị phân, $f(\mathbf{X})$ là một xâu nhị phân độ dài $n$, do đó $S_{\mathcal{F}}(\mathbf{X}) \leq 2^n$. Họ mô hình $\mathcal{F}$ được gọi là phá vỡ tập dữ liệu $\mathbf{X}$, nếu $S_{\mathcal{F}}(\mathbf{X}) = 2^n$. Nghĩa là với mọi cách gán nhãn ngẫu nhiên cho tập dữ liệu $\mathbf{X}$, luôn tìm được một mô hình $f \in \mathcal{F}$ có thể khớp hoàn hảo tập dữ liệu với sai số bằng 0.
Hệ số phá vỡ kích thước $n$ (shatter coefficient hoặc còn gọi là growth function), ký hiệu $S_{\mathcal{F}}(n)$ là số lượng hành vi tối đa mà họ mô hình $\mathcal{F}$ có thể tác động lên các tập dữ liệu gồm $n$ điểm:
$$ S_{\mathcal{F}}(n) \triangleq \max\limits_{\mathbf{X} = \{x_1, x_2, \ldots, x_n\}} S_{\mathcal{F}}(\mathbf{X}) \tag{11} $$
Số chiều VC (Vapnik-Chervonenkis dimension) của họ mô hình $\mathcal{F}$, ký hiệu là $VC_{\mathcal{F}}$, được xác định như sau:
$$ VC_{\mathcal{F}} \triangleq \max\{n : S_{\mathcal{F}}(n) = 2^n\} \tag{12}$$
Như vậy số chiều VC của họ mô hình $\mathcal{F}$ là kích cỡ tập dữ liệu lớn nhất mà ta có thể bố trí (lựa chọn) để họ mô hình $\mathcal{F}$ phá vỡ được chúng. Độ đo $VC_{\mathcal{F}}$ thể hiện mức độ đa dạng của họ mô hình $\mathcal{F}$.
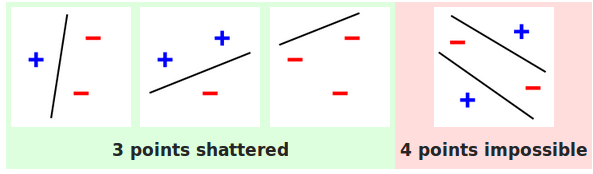
Ví dụ xét họ mô hình tuyến tính trên mặt phẳng 2D, tức là họ các đường thẳng (xem Hình 2). Họ mô hình $\mathcal{F}$ này có thể phá vỡ kích thước $n = 3$ vì ta có thể chỉ ra 3 điểm trên mặt phẳng mà với mọi cách gãn nhãn cho 3 điểm này ta đều có thể phân tách chúng thành 2 lớp bằng một đường thẳng $f$. Tuy nhiên với kích thước $n=4$, ta không thể chỉ ra 4 điểm nào để họ mô hình này có thể phá vỡ. Vì vậy số chiều VC của họ mô hình tuyến tính trên không gian 2D là bằng 3.
Tổng quát lên, họ các siêu phẳng trong không gian $k$ chiều có số chiều VC là $k + 1$.
2.2. Độ phức tạp Ramechader
Độ phức tạp Ramechader thực nghiệm của họ mô hình $\mathcal{F}$ trên tập huấn luyện $\mathbf{X} = \{x_1, x_2, \ldots, x_n\}$ được định nghĩa như sau:
$$ \widehat{Rad}_n(\mathcal{F}) \triangleq \mathbb{E}_\delta\big[ \sup\limits_{f \in \mathcal{F}} \frac{1}{n}\sum_{i=1}^{n}\delta_i f(x_i) \big] \tag{13}$$
trong đó $\delta_1,\ldots,\delta_n$ là các biến ngẫu nhiên phân phối đều trên tập giá trị $\{ \pm 1\}$, gọi là các biến ngẫu nhiên Ramechader.
Độ phức tạp Ramechader của họ mô hình $\mathcal{F}$ được định nghĩa như sau:
$$ Rad_n(\mathcal{F}) \triangleq \mathbb{E}_\mathbf{X}\big[ \widehat{Rad}_n(\mathcal{F}) \big] \tag{14}$$
Độ phức tạp Ramechader thực nghiệm $\widehat{Rad}_n(\mathcal{F})$ thể hiện khả năng khớp của họ mô hình $\mathcal{F}$ với $n$ nhiễu ngẫu nhiên Ramechader $\delta_1,\ldots,\delta_n$.
3. Lý thuyết cổ điển đánh giá khả năng tổng quát hóa của mô hình và hạn chế
3.1. Đánh giá cận trên sai số ước lượng
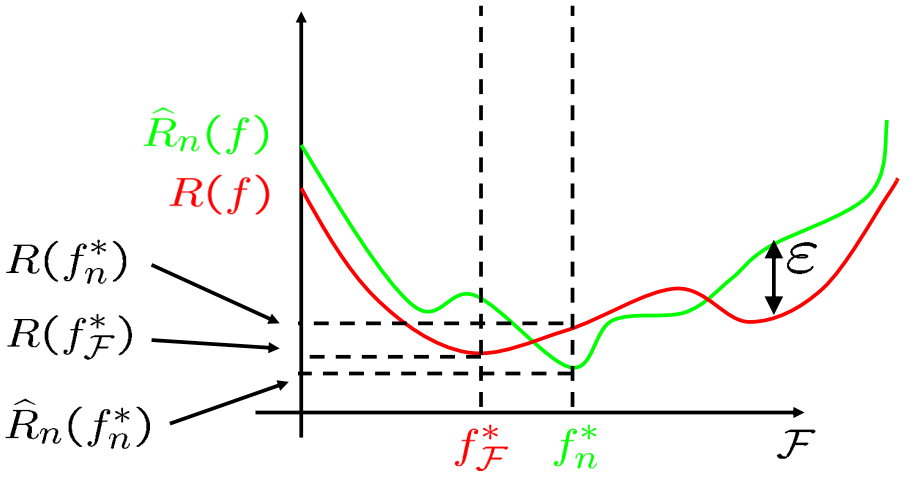
Ta ký hiệu $\epsilon$ là cận trên đúng của khoảng cách tổng quát hóa:
$$ \epsilon = \sup\limits_{f \in \mathcal{F}} |\Delta R(f)| = \sup\limits_{f \in \mathcal{F}} |R(f) – \hat{R}_n(f)| $$
Ta có:
$$ R(f^*_n) \leq \hat{R}_n(f^*_n) + \epsilon \leq \hat{R}_n(f^*_\mathcal{F}) +\epsilon \leq R(f^*_\mathcal{F}) + \epsilon + \epsilon = R(f^*_\mathcal{F}) + 2 \epsilon $$
Do đó, ta có đánh giá cận trên sai số ước lượng như sau:
$$ R(f^*_n) – R(f^*_\mathcal{F}) \leq 2 \epsilon = 2 \sup\limits_{f \in \mathcal{F}} |\Delta R(f)| \tag{15}$$
Như vậy để đánh giá cận trên cho sai số ước lượng trong Công thức (\ref{eq9}), ta chỉ cần đánh giá cận trên cho khoảng cách tổng quát hóa $|\Delta R(f)|$ như trong phần 3.2 dưới đây.
3.2. Lý thuyết cổ điển đánh giá cận trên khoảng cách tổng quát hóa
3.2.1. Họ hữu hạn các mô hình
Trong trường hợp họ mô hình là hữu hạn, ta có thể đánh giá trực tiếp cận trên khoảng cách tổng quát hóa bằng định lý dưới đây.
Định lý 1: Giả sử họ mô hình $\mathcal{F}$ là hữu hạn và hàm chi phí $L$ có miền giá trị bị chặn trong khoảng [0, 1], tức là $0 \leq L(f(x), y) \leq 1$, $n$ là kích thước tập huấn luyện. Khi đó với mọi $\delta$ thỏa mãn $0 < \delta < \frac{1}{2}$ và với mọi mô hình $f \in \mathcal{F}$, ta sẽ có bất đẳng thức sau với xác suất đúng ít nhất bằng $1 – \delta$:
$$ |\Delta R(f)| \leq \sqrt{\frac{log|\mathcal{F}|+log(2/\delta)}{2n}} \tag{16} \label{eq16}$$
3.2.2. Họ vô hạn các mô hình
Khi lực lượng của họ mô hình $\mathcal{F}$ là vô hạn, đánh giá cận trên theo Công thức (\ref{eq16}) trở nên vô nghĩa do vế phải của Công thức (\ref{eq16}) bằng $\infty$. Vì vậy ta cần một đánh giá cận trên khác có ý nghĩa trong trường hợp này.
Định lý 2: Giả sử $\mathcal{F}$ là một họ mô hình, $L(\mathcal{F}) = \{L_f : f \in \mathcal{F}\}$ là tập các hàm chi phí của các mô hình, trong đó $L_f(x, y) = L(f(x), y)$ bị chặn trong khoảng [0, 1], tức là $0 \leq L(f(x), y) \leq 1$, $n$ là kích thước tập huấn luyện. Khi đó với mọi $\delta$ thỏa mãn $0 < \delta < 1$ và với mọi mô hình $f \in \mathcal{F}$, ta sẽ có bất đẳng thức sau với xác suất đúng ít nhất bằng $1 – \delta$:
$$ Generalization~gap= \Delta R(f) \leq 2 \widehat{Rad}_n(L(\mathcal{F})) + 3 \sqrt{\frac{log \frac{2}{\delta} }{n}} \tag{17} \label{eq17} $$
Nếu hàm chi phí có dạng 0/1, tức là $L(f(x), y) =\mathbb{I}(f(x) \neq y) = \frac{1-y \cdot f(x)}{2}$, khi đó: $$\widehat{Rad}_n(L(\mathcal{F})) = \widehat{Rad}_n(\mathcal{F})/2 \tag{18} \label{eq18} $$
Người ta có thể đánh giá cận của độ phức tạp Ramechader như sau:
$$ \widehat{Rad}_n(\mathcal{F}) \leq \sqrt{\frac{2 \cdot logS_{\mathcal{F}}(\mathbf{X})}{n}} \tag{19} \label{eq19} $$
trong đó $S_{\mathcal{F}}(\mathbf{X})$ là số hành vi khác nhau mà họ mô hình $\mathcal{F}$ có thể tác động lên tập huấn luyện $\mathbf{X}$ như định nghĩa ở Công thức (\ref{eq10}).
Giả sử họ mô hình $\mathcal{F}$ có số chiều VC là $d = {VC}_{\mathcal{F}} < \infty$. Sử dụng bổ đề Sauer, ta có:
$$ S_{\mathcal{F}}(\mathbf{X}) \leq \sum\limits_{k=1}^{d}C^k_n \leq \begin{cases} 2^n, \tt{if}~ n \leq d \\ \left(\frac{en}{d}\right)^d, \tt{if}~ n > d \end{cases} \tag{20} \label{eq20}$$
trong đó $e$ là cơ số tự nhiên.
Kết hợp các kết quả \ref{eq17}, \ref{eq18}, \ref{eq19}, \ref{eq20}, ta có:
$$ Generalization~gap= \Delta R(f) \leq \sqrt{\frac{2d\cdot log(\frac{en}{d})}{n}}+ 3 \sqrt{\frac{log \frac{2}{\delta} }{n}} \tag{21} \label{eq21} $$
3.3. Hạn chế lý thuyết cổ điển
Theo công thức (\ref{eq21}), khoảng cách tổng quát hóa tỉ lệ nghịch với kích thước tập huấn luyện và tỉ lệ thuận với độ phức tạp của họ mô hình. Nghĩa là họ mô hình các phức tạp (càng nhiều tham số) càng dễ bị quá khớp và có khả năng tổng quát hóa tệ. Tuy nhiên, đánh giá cận trong Công thức ($\ref{eq21}$) chỉ đúng trong trường hợp $n > d$, nghĩa là mô hình có độ phức tạp thấp hơn tập huấn luyện (underparameterized). Các mạng nơ-ron thường bị tham số hóa quá mức (overparameterized) và có số chiều VC rất lớn, nghĩa là $d \gg n$, vì vậy đánh giá theo Công thức ($\ref{eq21}$) không còn đúng nữa.
4. Tổng quát hóa của mạng nơ-ron: góc nhìn hiện đại
4.1. Khớp nhiễu ngẫu nhiên và nhãn ngẫu nhiên
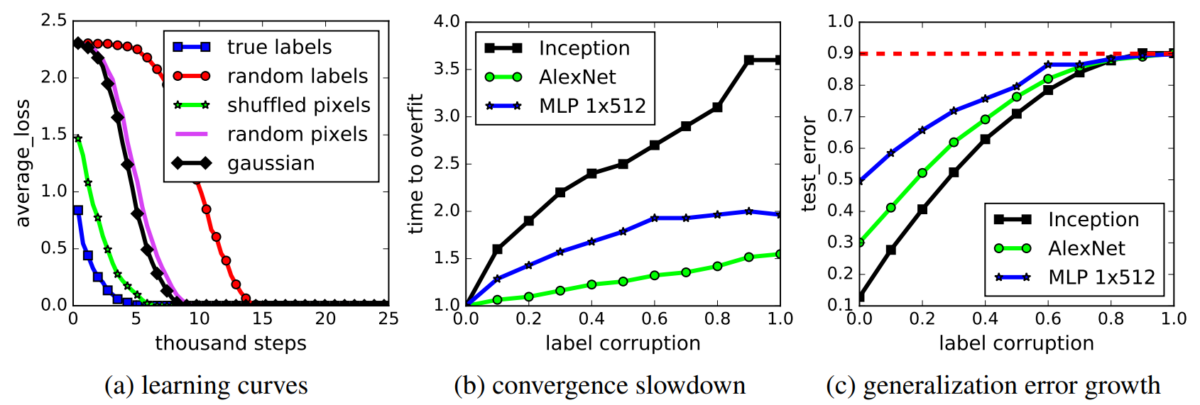
Nghiên cứu trong [2] đã chỉ ra rằng mạng nơ-ron dễ dàng khớp các tập dữ liệu, thậm chí cả khi ta thực hiện thêm nhiễu ngẫu nhiên vào dữ liệu và gán nhãn ngẫu nhiên cho chúng. Điều này chứng tỏ độ phức tạp của mạng nơ-ron là rất lớn và dễ dàng “phá vỡ” các tập huấn luyện.
4.2. Vai trò của chính quy hóa đối với khả năng tổng quát hóa của mạng nơ-ron
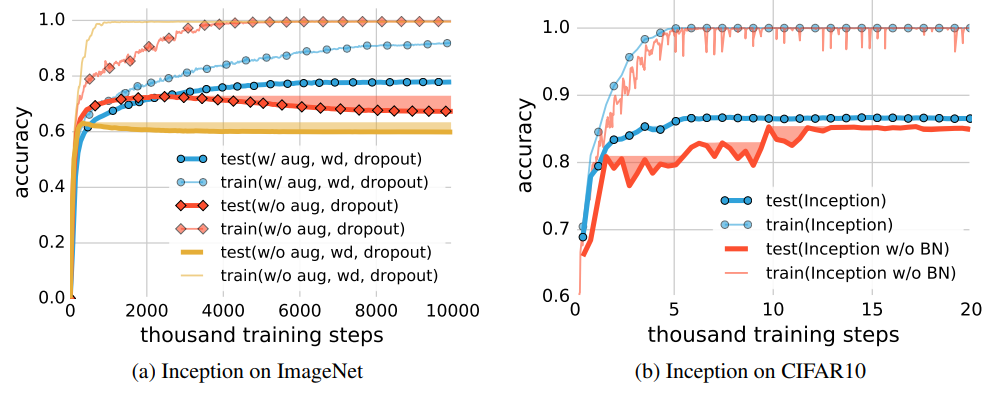
Nghiên cứu trong [2] chỉ ra áp dụng các kỹ thuật chính quy hóa với mạng nơ-ron, như tăng cường dữ liệu (augmentation), giảm trọng số (weight decay), BN, dropout, có tác dụng tăng khả năng tổng quát hóa nhưng sự cải thiện là không đáng kể. Hình 5a thể hiện khi không áp dụng kỹ thuật chính quy hóa nào, mạng vẫn tổng quát hóa rất tốt (đường màu vàng), chỉ tệ hơn một chút so với khi áp dụng. Hình 5b thể hiện BN có tác dụng cải thiện tính tổng quát hóa của mạng và làm ổn định quá trình huấn luyện (đường màu xanh mượt hơn, không bị dao động mạnh ở giai đoạn đầu như đường màu cam). Điều này hoàn toàn trái ngược với các lý thuyết học máy cổ điển, trong đó kỹ thuật chính quy hóa đóng vai trò rất quan trọng trong việc chống overfitting.
4.3. Double descent: Hiện tượng hạ kép
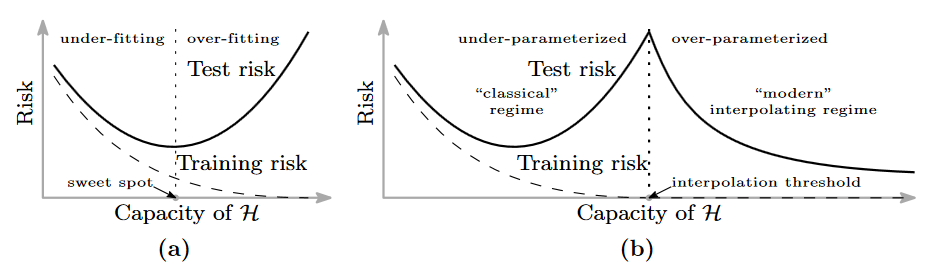
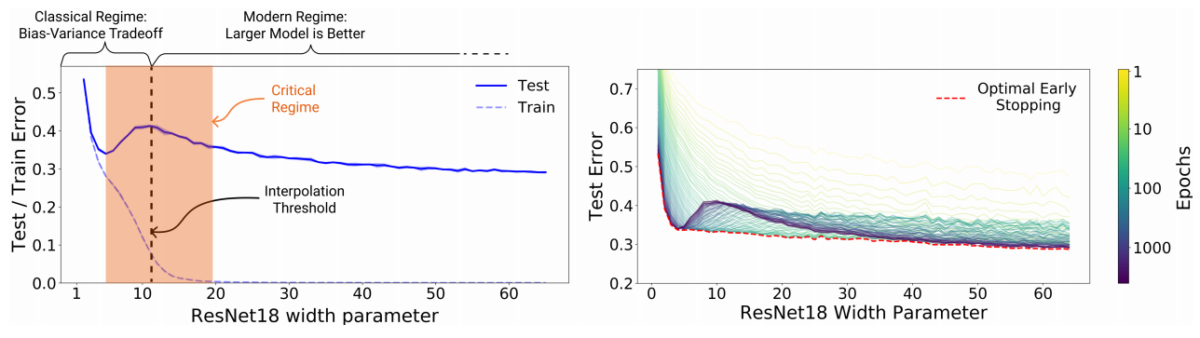
Hiện tượng hạ kép (Double descent) hay còn gọi là benigh overfit lần đầu tiên được phát hiện bởi Belkin và cộng sự trong [3]. Lý thuyết học máy cổ điển cho rằng mô hình càng lớn càng dễ bị quá khớp và có khả năng tổng quát hóa kém, nhưng [3] đã chỉ ra rằng các mô hình càng lớn càng tốt hơn. Nghiên cứu [3] phát hiện ra rằng bức tranh cổ điển về sự cân bằng độ thiên lệch và phương sai (bias-variance trade off) sẽ bị phá vỡ tại thời điểm khi sai số huấn luyện xấp xỉ 0 mà Belkin gọi là ngưỡng nội suy (Interpolation threshold). Trước ngưỡng nội suy, sự cân bằng độ thiện lệch và phương sai được đảm bảo, và độ phức tạp của mô hình càng tăng sẽ dẫn đến hiện tượng học quá khớp, làm tăng sai số kiểm thử (Hình 6a). Tuy nhiên, sau ngưỡng nội suy, họ nhận thấy rằng lỗi kiểm thử bắt đầu giảm xuống khi tiếp tục tăng độ phức tạp của mô hình (Hình 6b). Hiện tượng hạ kép không chỉ xảy ra với các mạng nơ-ron mà cũng xảy ra với các mô hình học máy cổ điển dạng ensemble và boosting nói chung như Random Forest hay AdaBoost [3, 4]. Với các mô hình học máy cổ điển đơn giản hơn như mô hình hồi quy tuyến tính [12, 13], hồi quy với đặc trưng ngẫu nhiên [14], hiện tượng hạ kép có thể chứng minh bằng lý thuyết.
4.4. Giả thuyết tấm vé xổ số – Lottery Ticket Hypothesis
Cắt tỉa mạng nơ-ron (prunning) ngày càng có nhiều ứng dụng thực tế trong học sâu, giúp chúng ta nén các mạng nơ-ron thành bé hơn nhiều lần mà độ chính xác gần như không suy hao. Nhiều thử nghiệm đã chỉ ra rằng, dù cắt tỉa 90% đến 99% tham số của nhiều mạng thì độ chính xác cũng chỉ giảm 1-2%. Tại sao lại như vậy?
Nghiên cứu [5] đã đưa ra giả thuyết về tấm vé xổ số như sau:
Một mạng nơ-ron lớn được khởi tạo ngẫu nhiên luôn chứa một mạng con được khởi tạo “may mắn” mà khi được huấn luyện độc lập thì mạng con sẽ đạt được khả năng tổng quát hóa ngang ngửa mạng cha sau số bước lặp gần như bằng nhau.
Nói cách khác, mạng nơ-ron lớn giống như một hộp quà to với rất nhiều giấy lộn vô giá trị trong đó để bọc một phần quá nhỏ giá trị cao trong đó – chính là mạng con nêu trên. Việc cắt tỉa mạng nơ-ron cha cũng tương tự như việc bóc hộp quà để lấy phần quà trong đó. Tác giả trong [5] cho những mạng con này đã giành tấm vé chiến thắng trong trò xổ số “khởi tạo trong số”. Khi khởi tạo mạng cha, các mạng nơ-ron con cũng được khởi tạo theo và một số mạng con may mắn được khởi tạo trọng số “phù hợp” với bài toán và đóng vai trò chính trong quá trình huấn luyện. Thuật toán SGD dường như chỉ tập trung vào mạng con chiến thắng và bỏ qua phần còn lại của mạng cha.
Mạng nơ-ron lớn chỉ đóng vai trò lúc khởi tạo để sinh ra rất nhiều mạng con ngẫu nhiên. Khi mạng cha càng lớn, số mạng con càng nhiều và xác suất càng cao sẽ có một mạng con may mắn giành được tấm vé chiến thắng. Đó là lý do tại sao mạng càng lớn càng dễ huấn luyện và có khả năng tổng quát hóa tốn hơn như hiện tượng hạ kép nêu trên.
Tuy nhiên có một vấn đề là đa số phần còn lại của mạng cha không đóng góp vào quá trình học nhưng vẫn tiêu toán rất nhiều chi phí tài nguyên tính toán. Vì vậy cần một phương pháp tiếp cận hiệu quả hơn là việc cứ tăng kích thước mạng mãi để hy vọng tìm chiếc vé chiến thắng.
4.5. Hố cực tiểu phẳng là dấu hiệu tổng quát hóa tốt?
Một cách giải thích khác về vấn đề tổng quát hóa tốt của mạng nơ-ron lớn chính là sự thần kỳ của thuật toán SGD. Bản thân thuật toán SGD đóng vai trò như một kỹ thuật chính quy hóa không tường minh [2]. Thuật toán SGD biết cách đề tìm cách hố cực tiểu thoải (flat), thay vì các hố cực tiểu nhọn (sharp). Nghiên cứu [6] cho rằng các hố cực tiểu thoải thường có khả năng tổng quát hóa tốt hơn. Mặt khác, nghiên cứu [7] nói rằng hố cực tiểu nhọn cũng cũng có thể tổng quát hóa tốt, ngược lại hố cực tiểu thoải cũng có thể tổng quát hóa kém.
Tuy nhiên, xu thế chung đều cho rằng hố cực tiểu thoải có khả năng tổng quát hóa tốt hơn hố nhọn. Điều này khá hợp lý theo cảm nhận trực quan vì hố thoải sẽ ít bị dao động trong lân cận xung quanh cực tiểu vì gần như giữ nguyên giá trị hàm mục tiêu trong lân cận đó.
4.7. Đánh giá khả năng tổng quát hóa từ thể hiện của quá trình tối ưu
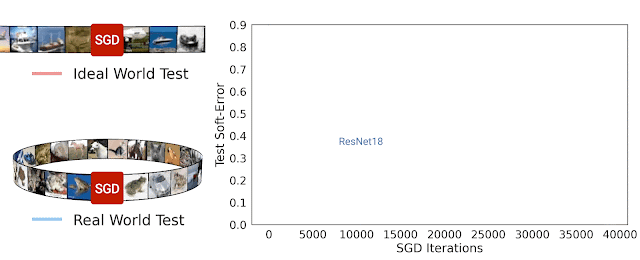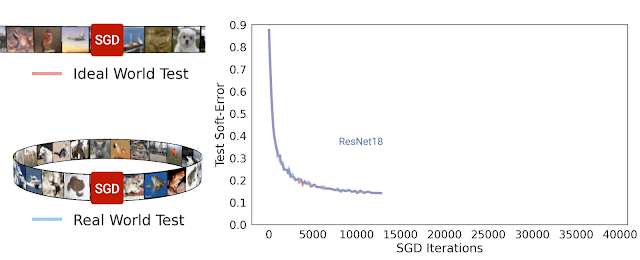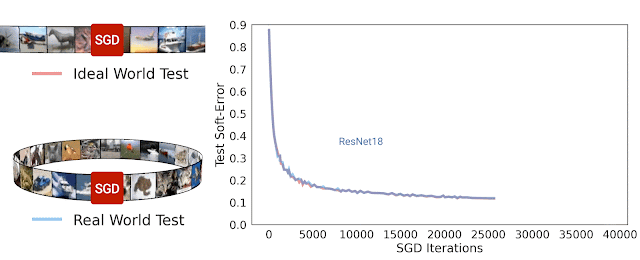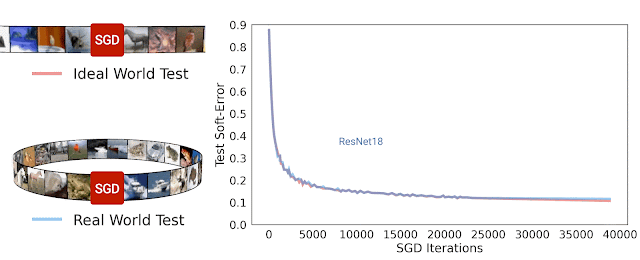
Trong nghiên cứu [8], nhóm tác giả đã đề xuất một phương pháp gọi là Deep Bootstrap Framework để đánh giá mối liên quan giữa khả năng tổng quát hóa với quá trình tối ưu. Tác giả định nghĩa thế giới thực (real world) là cách huấn luyện mô hình thông thường khi lặp đi lặp lại nhiều epoch với cùng tập huấn luyện như nhau. Thế giới lý tưởng là khi huấn luyện mô hình nhưng dữ liệu tại mỗi bước luôn mới, không bao giờ lặp lại. Để tạo “mô phỏng” thế giới lý tưởng, tác giả dùng mạng GAN để tạo ra 6 triệu ảnh huấn luyện từ tập gốc CIFAR10. Khi huấn luyện mô hình trên tập ảnh mới này với thời lượng không quá 1 epoch ta sẽ để tạo ra sự vô hạn ảo về dữ liệu, nghĩa là tại mỗi bước lặp đều dùng dữ liệu khác hẳn nhau. Thử nghiệm huấn luyện với mạng ResNet18 trên thế giới thực và thế giới lý tưởng cho kết quả rất ngạc nhiên khi chúng có sai số kiểm thử tương tự nhau. Dường như mô hình không quan tâm là nó đang nhìn thấy dữ liệu mới hay dữ liệu cũ đã từng thấy trước đó. Hiện tượng này cũng quan sát thấy đối với mạng MLP hay Vision Transfomer. Dựa trên quan sát thử nghiệm, tác giả nhận định rằng mạng nơ-ron có khả năng tổng quát hóa tốt nếu (1) tối ưu nhanh trên thế giới lý tưởng và (2) không tối ưu quá nhanh trên thế giới thực.
4.8. Một số đánh giá cận trên cho khoảng cách tổng quát hóa của mạng nơ-ron
Định lý dưới đây đánh giá độ phức tạp Rademacher của mạng nơ-ron hai lớp. Một số kết quả khác có thể xem trong [1] và [9-11].
Định lý 3: Giả sử:
- $x \in \mathbb{R}^d$ là véc-tơ đầu vào của mạng nơ-ron với độ dài bị chặn $||x||_2 \leq C$
- $w_j \in \mathbb{R}^d$ là trọng số nối với nơ-ron thứ $j$, $j = 1, 2, \ldots, m$
- $\alpha \in \mathbb{R}^m$ là trọng số nối các $m$ nơ-ron lớp ẩn với đầu ra
- $h: \mathbb{R} \rightarrow \mathbb{R}$ là hàm kích hoạt 1-Lipschitz thỏa mãn $h(0)=0$, ví dụ tanh hoặc ReLU.
- Với mỗi bộ trọng số $w, \alpha$, xây dựng một mạng nơ-ron như sau: $$ f_{w, \alpha} = \sum\limits_{j=1}^m \alpha_jh(w_jx) $$
- $\mathcal{F}$ là họ mạng nơ-ron với trọng số bị chặn: $$ \mathcal{F} = \{ f_{w, \alpha} : ||\alpha||_2 \leq B_{\alpha}, ||w_j||_2 \leq B_w \forall j = 1, \ldots, m \} $$
Khi đó:
$$ Rad_n(\mathcal{F}) \leq 2B_{\alpha} B_w C\sqrt{\frac{m}{n}} \tag{22}$$
Từ Định lý 3 ta thấy cận trên khả năng tổng quát hóa của mạng nơ-ron tỉ lệ thuận với độ dài của véc-tơ đầu vào và các véc-tơ trọng số, tỉ lệ thuận với số lượng nơ-ron và tỉ lệ nghịch với kích thước tập huấn luyện.
5. Kết luận
Lý thuyết học máy cổ điển chỉ chú trọng trường hợp mô hình được tham số hóa dưới mức (underparameterized). Khi mô hình được tham số hóa quá mức như trong các mạng nơ-ron, ta cần một lý thuyết học máy mới để giải thích. Đáng tiếc là hiện vẫn chưa có một lý thuyết trọn vẹn cho vấn đề này, và các nhà nghiên cứu trên thế giới vẫn đang tích cực tìm tòi và tranh cãi. Bài viết này cung cấp một số góc nhìn và giả định về lý thuyết mới mẻ này. Một số cách tiếp cận khác xem xét mạng nơ-ron dưới chế độ hàm nhân NTK (Neural Tangent Kernel) khi đẩy chiều rộng của mạng nơ-ron ra vô hạn [10, 11]. Ở chế độ này, mạng nơ-ron được tuyến tính hóa với hàm nhân NTK và có thể dùng các lý thuyết cổ điển để đánh giá khả năng tổng quát hóa của chúng.
Kết thúc bài viết, mời các bạn xem video ngắn gọn dưới đây tóm lược về góc nhìn lý thuyết học máy cổ điển và góc nhìn hiện đại.
Người viết: SangDV
6. Tài liệu tham khảo
1. CS229T Stanford – Statistical Learning Theory Notes: https://web.stanford.edu/class/cs229t/notes.pdf
2. Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, Oriol Vinyals: Understanding deep learning requires rethinking generalization. ICLR 2017
3. Belkin, M., Hsu, D., Ma, S., & Mandal, S.: Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences (2019), 116(32), 15849-15854.
4. Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever: Deep Double Descent: Where Bigger Models and More Data Hurt. ICLR 2020
5. Jonathan Frankle, Michael Carbin: The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. ICLR 2019
6. Nitish Shirish Keskar, Dheevatsa Mudigere, Jorge Nocedal, Mikhail Smelyanskiy, Ping Tak Peter Tang:
On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. ICLR 2017
7. Laurent Dinh, Razvan Pascanu, Samy Bengio, Yoshua Bengio: Sharp Minima Can Generalize For Deep Nets. ICML 2017: 1019-1028
8. Preetum Nakkiran, Behnam Neyshabur, Hanie Sedghi: The Deep Bootstrap Framework: Good Online Learners are Good Offline Generalizers. ICLR 2021
9. Kenji Kawaguchi, Leslie Pack Kaelbling, Yoshua Bengio: Generalization in Deep Learning. CoRR abs/1710.05468 (2017)
10. Daniel A. Roberts, Sho Yaida, Boris Hanin: The Principles of Deep Learning Theory. CoRR abs/2106.10165 (2021)
11. Julius Berner, Philipp Grohs, Gitta Kutyniok, Philipp Petersen: The Modern Mathematics of Deep Learning. CoRR abs/2105.04026 (2021)
12. Trevor Hastie, Andrea Montanari, Saharon Rosset, Ryan J. Tibshirani: Surprises in High-Dimensional Ridgeless Least Squares Interpolation. CoRR abs/1903.08560 (2019)
13. Peter L Bartlett, Philip M Long, Gabor Lugosi, and Alexander Tsigler: Benign overfitting in linear regression, Proceedings of the National Academy of Sciences 117 (2020), no. 48, 30063{30070.
14. Song Mei and Andrea Montanari: The generalization error of random features regression: Precise asymptotics and double descent curve, 2019, arXiv preprint arXiv:1908.05355.

