Understanding the Loss Landscape of DNNs

1. Hàm mục tiêu

Quá trình huấn luyện một mô hình học máy thường quy về bài toán tối ưu hóa hàm mục tiêu. Chẳng hạn, trong học máy có giám sát, hàm mục tiêu thường có dạng như sau:

$$\mathbf{J}(\theta, \textbf{D}) = \frac{1}{N}\sum_{i=1}^{N}L(f(\theta,x_i),y_i) \tag{1}$$

trong đó $\theta$ là tham số mô hình, $\textbf{D} = \{x_i,y_i\}_{i=1}^N$ là tập huấn luyện gồm $N$ mẫu dữ liệu và nhãn tương ứng, và $f$ là mô hình học máy.

Mục tiêu của huấn luyện mô hình học máy là xác định cực tiểu toàn cục của hàm mục tiêu: $\theta^* = \underset{\theta}{\operatorname{argmax}} \mathbf{J}(\theta, \textbf{D})$.

Tuy nhiên, hàm mục tiêu của mô hình học máy thực tế thường rất phức tạp, đặc biệt với các mạng nơ-ron hàng chục triệu biến, dẫn tới việc tìm kiếm cục tiểu toàn cục trong trường hợp tổng quát là không khả thi. Giải thuật SGD và các biến thể thường được sử dụng trong các trường hợp này để tìm ra lời giải xấp xỉ đủ tốt. Khi hàm càng phức tạp, giải thuật SGD càng khó hoạt động hiệu quả, dễ bị tắc sớm tại các hố cực tiểu địa phương nông (weak local minima).

2. Tính chất hàm mục tiêu mạng nơ-ron

Mạng nơ-ron có thể chứa hàng trăm triệu tham số. Vì vậy hàm mục tiêu của chúng thường rất phức tạp (Hình 1) với rất nhiều điểm cực trị. Đây là một thách thức cho các giải thuật SGD, đặc biệt nếu số điểm cực tiểu địa phương yếu chiếm đa số trên bề mặt hàm.

Bề mặt hàm mục tiêu của mạng nơ-ron có bị áp đảo bởi các điểm cực tiểu yếu hay không vẫn là một câu hỏi mở. Tuy nhiên hiện tại nhiều chuyên gia cho rằng với mạng nơ-ron đủ lớn, các cực tiểu địa phương của hàm sẽ chủ yếu là cực tiểu mạnh, nghĩa là giá trị của hàm tại các điểm cực tiểu này rất gần với giá trị tối ưu toàn cục [1]. Vì vậy việc huấn luyện mạng nơ-ron không phải là vấn đề quá “ác mộng” như trước đây nhiều người vẫn nghĩ.

Một lý do nữa giúp việc huấn luyện mạng nơ-ron dễ thành công đó là nhờ tính chất đối xứng của không gian tham số. Chúng ta dễ dàng đạt được các mô hình mạng tương đương nhau bằng cách hoán vị các tham số của mạng mà không ảnh hưởng gì kết quả đầu ra các các lớp. Ví dụ với mạng nơ-ron có $m$ lớp và mỗi lớp có $n$ nơ-ron sẽ có tất cả $n!^m$ cách hoán vị các tham số trong lớp. Điều này nghĩa là mỗi bộ tham số $\theta$ sẽ có $n!^m$ bộ tham số khác tương đương cùng cho một giá trị như nhau với hàm mục tiêu. Nếu $n = 20, m = 10$, $n!^m = (20!)^{10} \approx 10^{180}$, tức là mỗi bộ tham số có hơn $10^{180}$ bộ chất lượng tương đương, con số này còn nhiều hơn rất rất nhiều lần toàn bộ số nguyên tử trong vũ trụ hiện nay ước tính cỡ khoảng $10^{80}$. Chính vì vậy lời giải tốt trong không gian tham số của mạng nơ-ron tồn tại khắp nơi và ta không khó để tìm được chúng dù điểm xuất phát thường được khởi tạo ngẫu nhiên.

Có giả thuyết cho rằng mô hình học máy khi tăng số lượng tham số sẽ phải đối mặt với “lời nguyền của số chiều không gian” do sự bùng nổ về số lượng cấu hình tham số và rất khó để huấn luyện, đồng thời dễ bị hiện tượng học quá khớp (overfitting). Tuy nhiên điều này dường như không đúng với mạng nơ-ron. Giả thuyết “phước lành của số chiều không gian” cho rằng mạng nơ-ron càng lớn càng gia tăng số lượng cực tiểu tốt và càng dễ huấn luyện. Các cực tiểu tốt tồn tại rất nhiều trong không gian và có khả năng tổng quát hóa tốt. Dù khởi tạo ở điểm nào trong không gian thì xác suất rất cao ta vẫn dễ dàng tìm được đường đi tới hố cực tiểu tốt gần đó.

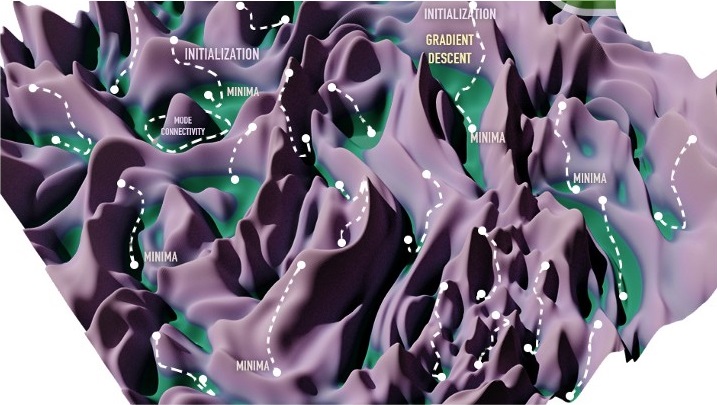
3. Sự liên thông giữa các hố cực tiểu

Trước đây, nhiều người vẫn nghĩ rằng các hố cực tiểu địa phương thường nằm độc lập với nhau. Muốn di chuyển từ hố này sang hố khác bắt buộc phải đi qua vùng địa hình cao. Ví dụ [2] sử dụng chiến thuật thay đổi tốc độ học theo hàm cosine để bắn lên cao thoát khỏi các hố cực tiểu địa phương và di chuyển sang hố mới (Hình 3).

Tuy nhiên, nghiên cứu gần đây [3] đã khám phá ra rằng các hố cực tiểu của mạng nơ-ron liên thông với nhau bằng các đường hầm dưới thấp (xem Hình 4 hoặc video chi tiết). Các mô hình (weights/checkpoints) của mạng dọc theo đường hầm thường cho giá trị hàm mục tiêu ngang bằng nhau và có độ chính xác gần như tương đương nhau trên tập huấn luyện và tập test. Các mô hình mạng dọc theo đường hầm dù có hiệu năng tương đương nhưng khả năng biểu diễn rất khác nhau, do vậy có thể kết hợp với nhau (ensemble) để gia tăng độ chính xác chung của mạng.

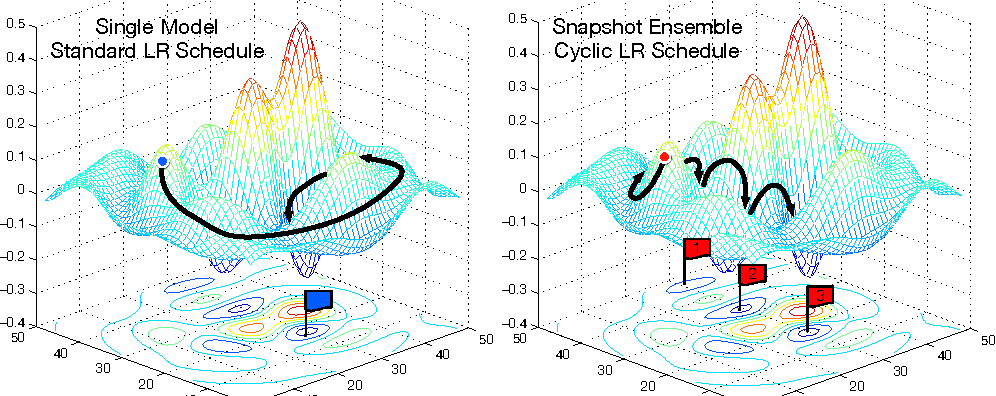
Ngoài ra, bề mặt vùng cao của hàm thường gập ghềnh. Tuy nhiên khi xuống vùng thấp, chẳng hạn như xung quanh đường hầm kết nối các hố cực tiểu, bề mặt hàm mục tiêu thường có xu hướng trơn mượt hơn.

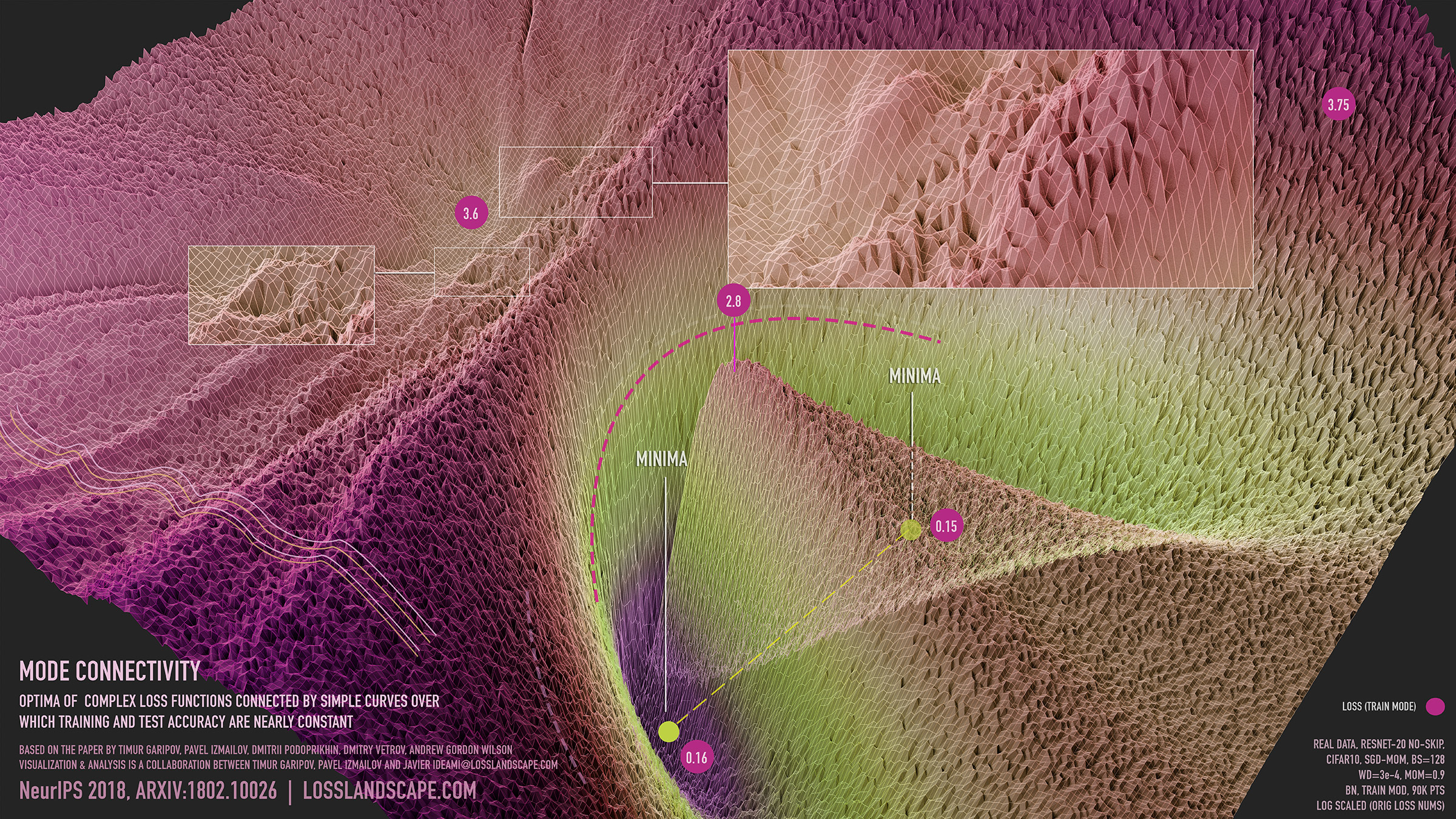
Hình 4. Sự liên thông giữa các hố cực tiểu [3, 11]

4. Các phương pháp làm mượt bề mặt hàm mục tiêu mạng nơ-ron

4.1. Hàm kích hoạt

Làm mượt hàm mục tiêu có vai trò quan trọng trong việc hỗ trợ SGD tìm được cực tiểu tốt. Các hàm kích hoạt khác nhau sinh ra các hàm mục tiêu với bề mặt có mức độ mượt khác nhau. Ở đây ta so sánh ảnh hưởng của 3 hàm kích hoạt sau:

$ReLU(x) = max(0, x)$

$Swish(x) = x \times sigmoid(x)$

$Mish(x) = x \times tanh(ln(1+e^x))$

Mạng nơ-ron sử dụng hàm kích hoạt ReLU [7], [8] thường có thể xấp xỉ bằng giao của một tập các siêu phẳng. Do đó, bề mặt hàm mục tiêu khi sử dụng ReLU (xem Hình 5) thường gồ ghề và gấp khúc đột ngột, gây ma sát lớn cản trở thuật toán SGD momentum vốn được ví như hiệu ứng viên bi nặng (heavy ball) lăn.

Trên Hình 6 thể hiện hàm mục tiêu của ResNet20 huấn luyện 200 epochs trên bộ CIFAR10 tương ứng với các hàm kích hoạt ReLU, Swish và Mish. Hàm ReLU sinh ra nhiều hố cực tiểu địa phương sâu và hẹp (narrow minima). Với địa hình này, thuật toán SGD gặp khó khăn do hoặc là dễ bị mắc ở các hố sâu lưng chừng (khi đó kết quả huấn luyện sẽ không đủ tốt), hoặc nếu may mắn thoát được các hố sâu lưng chừng cũng phải dùng tốc độ học rất nhỏ mới chui xuống được các hố sâu hơn, dẫn đến tốc độ hội tụ lâu hơn. Hàm Swish cải thiện đáng kể bề mặt hàm mục tiêu khi tạo những hố cực tiểu sâu hơn, rộng và phẳng hơn hẳn so với địa hình xung quanh. Tuy nhiên Swish vẫn tạo ra các hố cực tiểu lưng chừng có khả năng bẫy thuật toán SGD. Cuối cùng, hàm Mish cho hiệu quả đáng ngạc nhiên nhất khi tạo những hố cực tiểu rất sâu, rộng và phẳng (wide flat mimina) ở giữa, bao quanh là các hố cực tiểu rất nông và nhỏ, giúp SGD dễ dàng vượt qua.

Có thể nói, Mish là lựa chọn tốt để làm mượt bề mặt hàm mục tiêu huấn luyện. Nhược điểm của Mish so với ReLU là tính toán lâu hơn do phải tính hàm lũy thừa.

4.2. Sử dụng kết nối tắt

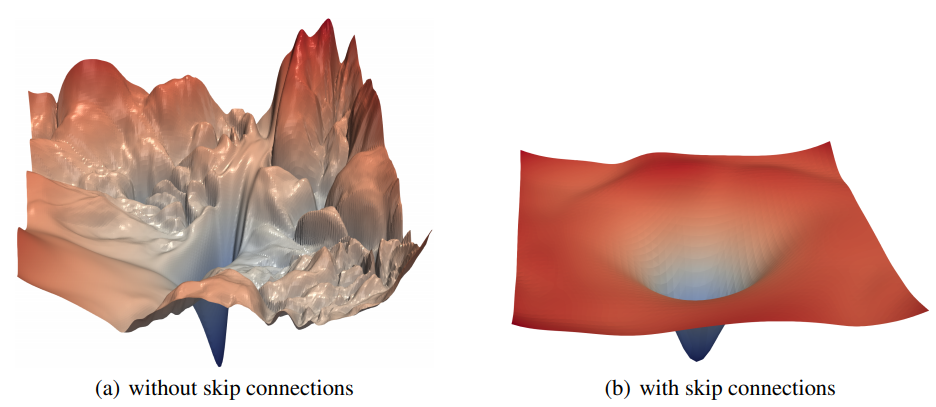
Kết nối tắt (skip connections) là thành phần quan trọng trong các mạng nơ-ron hiện đại. Khái niệm này lần đầu tiên được đề cập trong mạng ResNet, sau đó được sử dụng rộng rãi trong nhiều kiến trúc mạng khác. Kết quả biểu diễn trực quan [4] như trên Hình 7 hoặc trên video cho thấy rằng, mạng nơ-ron sử dụng kết nối tắt có bề mặt trơn mượt hơn nhiều so với những mạng nối tiếp (plain networks).  Với một số mạng nơ-ron cụ thể có sử dụng kết nối tắt, chẳng hạn mạng kết nối đầy đủ hai lớp ẩn dùng hàm kích hoạt ReLU, có thể chứng minh lý thuyết rằng, ngoài hố cực tiểu toàn cục, các hố cực tiểu còn lại thường rất nông [6].

 

4.3 Tấm vé chiến thắng, cắt tỉa mạng nơ-ron và sự thay đổi của bề mặt hàm mục tiêu

Cắt tỉa mạng nơ-ron (prunning) ngày càng có nhiều ứng dụng thực tế trong học sâu, giúp chúng ta nén các mạng nơ-ron thành bé hơn nhiều lần mà độ chính xác gần như không suy hao. Nhiều thử nghiệm đã chỉ ra rằng, dù cắt tỉa 90% đến 99% tham số của nhiều mạng thì độ chính xác cũng chỉ giảm 1-2%. Tại sao lại như vậy?

Nghiên cứu [9] đã đưa ra giả thuyết về tấm vé xổ số như sau:

Một mạng nơ-ron lớn được khởi tạo ngẫu nhiên luôn chứa một mạng con được khởi tạo “may mắn” trong đó mà khi được huấn luyện độc lập thì nó sẽ đặt được khả năng tổng quát hóa ngang ngửa mạng cha sau số bước lặp gần như bằng nhau.

Nói cách khác, mạng nơ-ron lớn giống như một hộp quà to với rất nhiều giấy lộn vô giá trị trong đó để bọc một phần quá nhỏ giá trị cao trong đó – chính là mạng con nêu trên. Việc cắt tỉa mạng nơ-ron cha cũng tương tự như việc bóc hộp quà để lấy phần quà trong đó. Tác giả trong [9] cho những mạng con này đã giành tấm vé chiến thắng trong trò xổ số “khởi tạo trong số”. Khi khởi tạo mạng cha, các mạng nơ-ron con cũng được khởi tạo theo và một số mạng con may mắn được khởi tạo trọng số “phù hợp” với bài toán và đóng vai trò chính trong quá trình huấn luyện. Thuật toán SGD dường như chỉ tập trung vào mạng con chiến thắng và bỏ qua phần còn lại của mạng cha.

Mạng nơ-ron lớn chỉ đóng vai trò lúc khởi tạo để sinh ra rất nhiều mạng con ngẫu nhiên. Khi mạng cha càng lớn, số mạng con càng nhiều và xác suất càng cao sẽ có một mạng con may mắn giành được tấm vé chiến thắng. Đó là lý do tại sao mạng càng lớn càng dễ huấn luyện và có khả năng tổng quát hóa tốn hơn như hiện tượng hạ kép nêu trên.

Tuy nhiên có một vấn đề là đa số phần còn lại của mạng cha không đóng góp vào quá trình học nhưng vẫn tiêu toán rất nhiều chi phí tài nguyên tính toán. Vì vậy cần một phương pháp tiếp cận hiệu quả hơn là việc cứ tăng kích thước mạng mãi để hy vọng tìm chiếc vé chiến thắng.

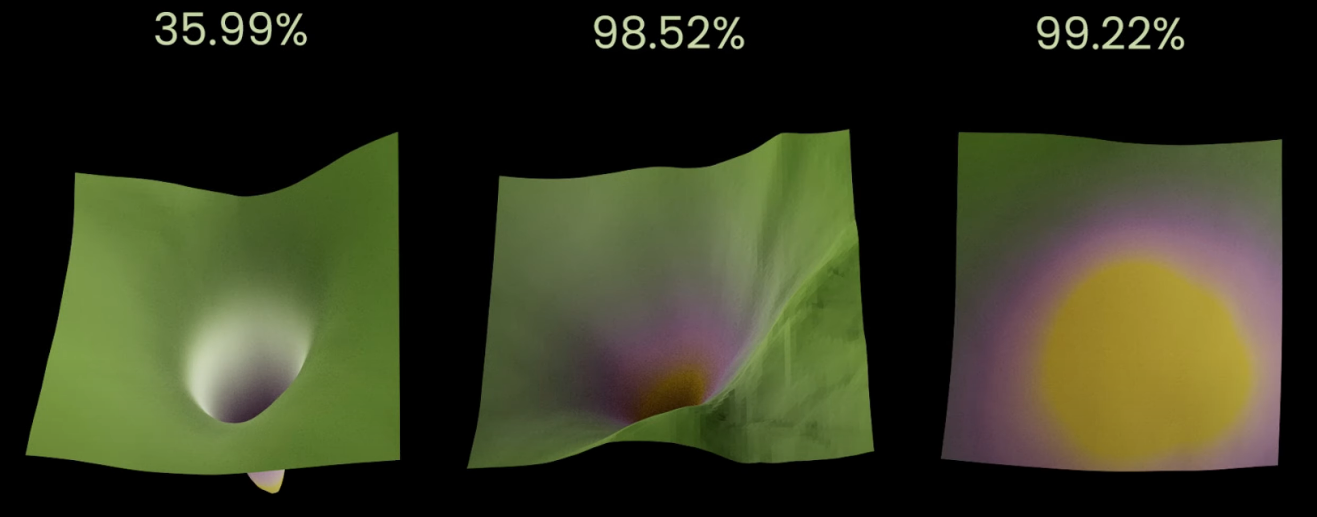
Như trên Hình 8, thử nghiệm cho thấy khi tỉ lệ càng cao thì bề mặt hàm mục tiêu càng rộng và phẳng, giúp các giải thuật tối ưu dễ dàng hội tụ hơn.

5. Phân tích độ mượt của hàm mục tiêu qua ống kính Hessian

To be continued… [10]

Để tìm hiểu thêm các thông tin chi tiết về bề mặt hàm mục tiêu, các bạn có thể đọc các tài liệu tham khảo [11], [12] và nghe Bài nói chuyện rất thú vị của tác giả Javier Ideami. Nhiều ý tưởng của bài viết và đa số hình vẽ đều được tham khảo và lấy trực tiếp từ các tài liệu gốc này của Javier Ideami và cộng sự.

Người viết: SangDV

6. Tài liệu tham khảo

1. Ian Goodfellow and Yoshua Bengio and Aaron Courville. Deep Learning. MIT Press, 2016.

2. Gao Huang, Yixuan Li, Geoff Pleiss, Zhuang Liu, John E. Hopcroft, Kilian Q. Weinberger. Snapshot Ensembles: Train 1, Get M for Free. ICLR (Poster) 2017

3. Timur Garipov, Pavel Izmailov, Dmitrii Podoprikhin, Dmitry P. Vetrov, Andrew Gordon Wilson. Loss Surfaces, Mode Connectivity, and Fast Ensembling of DNNs. NeurIPS 2018: 8803-8812

4. Diganta Misra. Mish: A Self Regularized Non-Monotonic Activation Function. BMVC 2020

5. Hao Li, Zheng Xu, Gavin Taylor, Christoph Studer, Tom Goldstein. Visualizing the Loss Landscape of Neural Nets. NeurIPS 2018: 6391-6401

6. Lifu Wang, Bo Shen, Ning Zhao, Zhiyuan Zhang. Is the Skip Connection Provable to Reform the Neural Network Loss Landscape? IJCAI 2020: 2792-2798

7. Boris Hanin, David Rolnick. Deep ReLU Networks Have Surprisingly Few Activation Patterns. NeurIPS 2019: 359-368

8. Thomas Laurent, James von Brecht. The Multilinear Structure of ReLU Networks. ICML 2018: 2914-2922

9. Jonathan Frankle, Michael Carbin. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. ICLR 2019

10. Zhewei Yao, Amir Gholami, Kurt Keutzer, Michael W. Mahoney. PyHessian: Neural Networks Through the Lens of the Hessian. IEEE BigData 2020: 581-590

11. Loss Landscape Project. URL: https://losslandscape.com/

12. Loss landscapes and the blessing of dimensionality. URL: https://towardsdatascience.com/loss-landscapes-and-the-blessing-of-dimensionality-46685e28e6a4