Contents
1. Kết nối tắt là gì?
Kết nối tắt là thành phần quan trọng trong hầu hết các kiến trúc nơ-ron tích chập (CNN) hiện đại, lần đầu được đề xuất trong ResNet [2]. Các mạng CNN trước đó như VGG thường có dạng thẳng (plain network), đầu ra một lớp là đầu vào cho lớp liền sau. Thử nghiệm cho thấy rằng độ chính xác của mạng VGG trên tập ImageNet tăng dần theo số lớp ẩn, nhưng đến một ngưỡng nào đó (khoảng 20 lớp) thì độ chính xác bắt đầu suy giảm. Đây gọi là hiện tượng suy biến của các mạng tích chập thẳng.
Điều này trái ngược với kết quả lý thuyết. Chẳng hạn [1] đã chỉ ra rằng, khả năng biểu diễn của mạng dùng hàm kích hoạt ReLU cỡ $O\left((C^d_n)^{(l – 1) \times d} \times n^d\right)$, trong đó $d$ là kích thước đầu vào, $n$ là độ rộng của mạng (số nơ-ron mỗi lớp ẩn), $l$ là chiều sâu của mạng (số lớp ẩn). Như vậy khả năng biểu diễu của mạng ReLU tăng lũy thừa theo độ sâu của mạng. Vì vậy lý do mạng bị suy biến khi quá sâu là do hàm phục tiêu quá phức tạp, bề mặt hàm hiểm trở và gây khó khăn cho các thuật toán tối ưu. Hoặc từ góc nhìn khác, mạng quá sâu dẫn tới hiện tượng triệt tiêu gradient làm các lớp ở xa hàm mục tiêu rất khó để học do không hiểu vài trò của chúng với hàm mục tiêu.
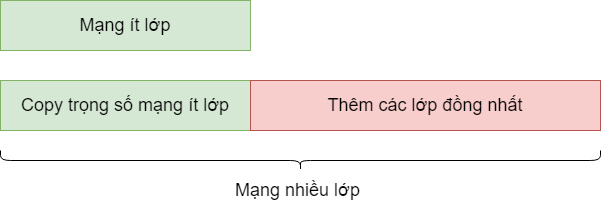
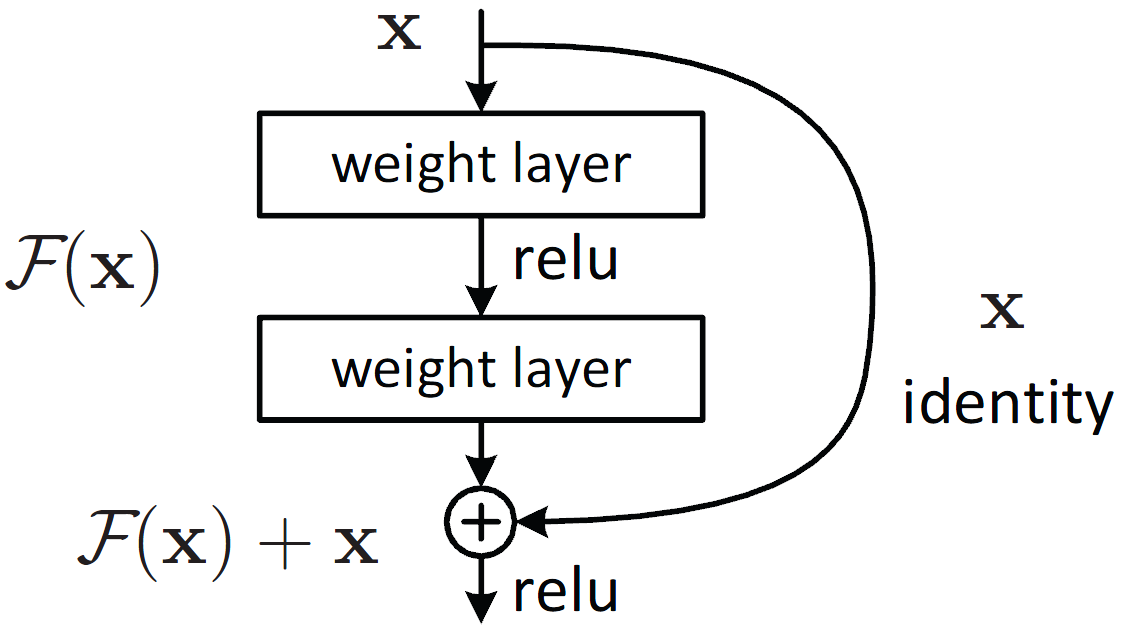
Về ý tưởng, nếu đã có một mạng nơ-ron tốt, ta hoàn toàn có thể dễ dàng xây dựng một mạng sâu hơn tùy ý với chất lượng tương đương bằng cách thêm các lớp đồng nhất (identity mapping) phía sau, nghĩa là các lớp có đầu ra giống hệt đầu vào (xem Hình 1). Bằng cách xây dựng như vậy, đầu ra của mạng ít lớp ban đầu và mạng nhiều lớp là giống hệt nhau. Do đó, nếu mạng nơ-ron biết cách học các lớp đồng nhất này thì có lẽ hiện tượng suy biến đã không xảy ra. Để giúp cho mạng nơ-ron học lớp đồng nhất một cách đơn giản, Kaiming He và cộng sự [2] đã đề xuất một “mẹo”, đó là học phần dư thông qua kiến trúc kết nối tắt. Thay vì học lớp nơ-ron biến đổi thẳng $x \rightarrow H(x)$, chỉ cần xây dựng lớp nơ-ron học phần dư $x \rightarrow F(x) = H(x)~-~x$, sau đó lấy $F(x)$ cộng với $x$ để đưa ra đầu ra $H(x)$ cuối cùng như mong muốn. Tuy về bản chất toán học không khác gì nhau, nhưng mẹo này trên thực tế hỗ trợ rất nhiều cho mạng nơ-ron khi nó muốn học ánh xạ đồng nhất. Thật vậy, nếu muốn học $x \rightarrow H(x) = x$, chỉ cần học lớp nơ-ron biến đổi $x \rightarrow H(x)~-~x = 0$. Với kiến trúc sử dụng ReLU mà [2] đề xuất như Hình 2, mạng chỉ cần đẩy các tham số của các lớp nơ-ron về 0 là thỏa mãn yêu cầu.
2. Các loại kết nối tắt và tác động tới quá trình huấn luyện
2.1. Phân loại kết nối tắt
Kết nối tắt thường chia thành hai loại ngắn và dài. Kết nối tắt ngắn dùng để nối các lớp nối tiếp nhau như trong ResNet [2] hoặc DenseNet [3], trong khi kết nối tắt dài thường sử dụng trong kiến trúc mã hóa – giải mã (encoder-decoder) như UNet [4]. Phần mã hóa trong các mạng này chứa nhiều biểu diễn mức thấp với nhiều thông tin chi tiết cục bộ, cho phép trả lời câu hỏi “ở đâu”. Phần giải mã chứa biểu diễn giàu ngữ nghĩa với thông tin toàn cục, cho phép trả lời câu hỏi “cái gì”. Kết nối tắt dài tổng hợp hai loại thông tin này với nhau, giúp chúng ta trả lời được cả hai câu hỏi “cái gì” và “ở đâu” một cách chính xác. Ngoài ra kết nối tắt cũng được sử dụng giữa cho các mạng đa luồng để giao thoa thông tin từ các tạp dữ liệu khác nhau [5].
2.2. Tác động tới quá trình huấn luyện
Bên cạnh nhiệm vụ truyền thông tin khi lan truyền tiến, kết nối tắt còn đóng vai trò quan trọng trong việc hạn chế hiện tượng triệt tiêu gradient. Chính các đường kết nối tắt này là “xa lộ”/hotline cho phép tín hiệu gradient có đường truyền trực tiếp nguyên vẹn từ hàm mục tiêu tới các lớp nơ-ron ở xa, trái ngược với việc lan truyền tuần tự qua từng lớp và bị suy hao dần như trong các mạng nơ-ron thẳng. Nhờ vậy các mạng sâu có thể dễ dàng học hơn nhờ kết nối tắt.
Ngoài ra, nhiều công trình nghiên cứu thực nghiệm đã chỉ ra rằng kết nối tắt làm mượt hàm mục tiêu và giúp cho các giải thuật tối ưu dễ dàng đạt được các điểm cực tiểu tốt trong không gian. Để hiểu rõ hơn, các bạn có thể tham khảo thêm bài blog: Understanding the Loss Landscape of DNNs.
3. Mối liên quan giữa kết nối tắt và kết hợp mô hình (model ensemble)
Nghiên cứu [6] đã chỉ ra rằng kiến trúc kết nối tắt có nhiều nét tương đồng với phương pháp kết hợp mô hình. Một mạng có $n$ kết nối tắt có thể phân rã thành nhiều $2^n$ “mô hình con” là các đường tính toán nối từ đầu vào tới đầu ra của mạng.

Ví dụ xét mạng có 3 kết nối tắt với các khối nơ-ron biến đổi ở giữa ký hiệu lần lượt là $f_1, f_2, f_3$ như Hình 3. Khi đó ta có:
$y_3 = f_3(y_2) + y_2 = f_3(f_2(y_1) + y_1) + f_2(y_1) + y_1$
$ = f_3(f_2(f_1(y_0) + y_0) + f_1(y_0) + y_0) + f_2(f_1(y_0) + y_0) + f_1(y_0) + y_0$
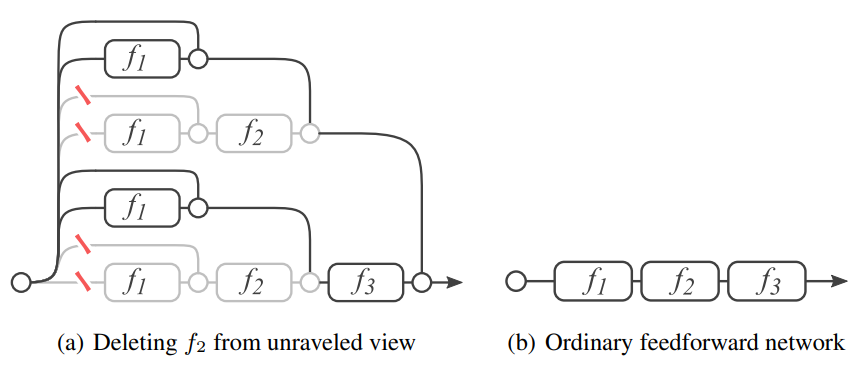
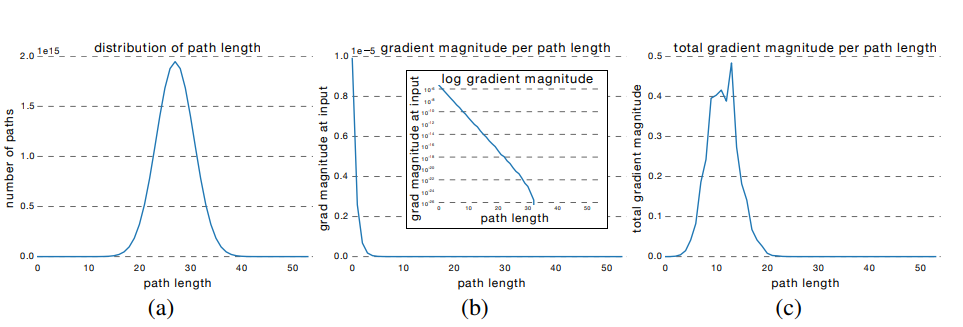
Nếu trải mạng phần dư này ra như trên Hình 4, ta thấy có $2^3 = 8$ đường khác nhau nối từ $y_0$ tới $y_3$. Tổng quát lên, nếu mạng có $n$ kết nối tắt sẽ có $2^n$ đường như vậy.
Trong các mạng nơ-ron thẳng, khi xóa một lớp bất kỳ thường làm mạng hỏng hoàn toàn và gần như không làm việc được sau khi xóa. Tuy nhiên nếu xóa một vài $k$ lớp ra khỏi mạng phần dư (Hình 4) thì vẫn còn $2^{n-k}$ đường tính toán khác và sai số của mạng thay đổi không nhiều. Khi $k$ tăng thì sai số tăng theo rất mượt mà, điều này rất giống trong kết hợp mô hình (model ensemble).
4. Từ mạng phần dư tới mạng nơ-ron phương trình vi phân thường (Neural ODE)
4.1. Mô hình hóa dữ liệu
Giả sử ta cần giải một bài toán xử lý dữ liệu có đầu vào $x$, và đầu ra $y$. Cách tiếp cận thông thường là xây dựng mô hình $f$ biểu diễn mối quan hệ trực tiếp giữa hai đại lượng $x \rightarrow y = f(x)$. Với các tiếp cận vi phân [7], ta sẽ xây dựng một mô hình $f$ biểu diễn tốc độ thay đổi của $y$ theo $x$, tức là $\frac{dy}{dx} = f(x, y)$. Do mạng nơ-ron có thể biểu diễn bất kỳ quan hệ liên tục phức tạp nào nên ta có thể dùng chúng để xấp xỉ tốc độ thay đổi của $y$ theo $x$.
Giả sử $h(t)$ là một hàm biến đổi liên tục từ đầu vào $x$ thành đầu ra $y$ sao cho $h(t_0) = x$ và $h(t_N) = y$, với $t_0$ và $t_N$ là hai tham số. Khi đó bài toán quy về huấn luyện một mạng nơ-ron $f$ để xấp xỉ đạo hàm của $h(t)$:
$\frac{dh(t)}{dt} = f(t, h(t), \theta_t),~~~~~~~~~~(1)$
trong đó $\theta_t$ là tham số của mạng nơ-ron ở lớp thứ $t$.
Các tham số $t_0$, $t_N$ và $\theta_t$ được học trong quá trình huấn luyện thông qua giải thuật lan truyền ngược [7].
4.2. Mối liên quan với mạng phần dư
Để giải xấp xỉ phương trình vi phân trên, ta có thể sử dụng phương pháp Euler thuận như sau:
$h(t_{n+1}) = h(t_n) + \delta_t f(t_n, h(t_n), \theta_{t_n}), n = 0, 1, \ldots, N-1~~~~~~~~~~(2)$
trong đó $\{t_0, t_1, …, t_N\}$ là dãy các thời điểm rời rạc cách đều nhau một khoảng $\delta_t$. Sai số của phương pháp Euler thuận tỉ lệ nghịch với $\delta_t$.
Nếu chọn $t_0 = 0, t_1 = 1, …, t_N = N$, ta có công thức:
$h(n+1) = h(n) + f(n, h(n), \theta_{n}).~~~~~~~~~~(3)$
Công thức (3) chính là kết nối tắt trong mạng phần dư, trong đó $f(n, h(n), \theta_{n})$ là lớp nơ-ron thứ $n$ với đầu vào $h(n)$ và tham số $\theta_{n}$. Trong trường hợp này, mạng nơ-ron $f$ trở thành một mạng phần dư có $N$ kết nối tắt với lớp thứ 0 là đầu vào $h(0) = x$ và lớp cuối cùng là kết quả đầu ra $h(N) = y$. Do đó mạng phần dư càng sâu thì bước $\delta_t$ càng nhỏ và mạng càng biểu diễn chính xác hàm $h(t)$.
4.3. Mạng phần dư vô hạn lớp
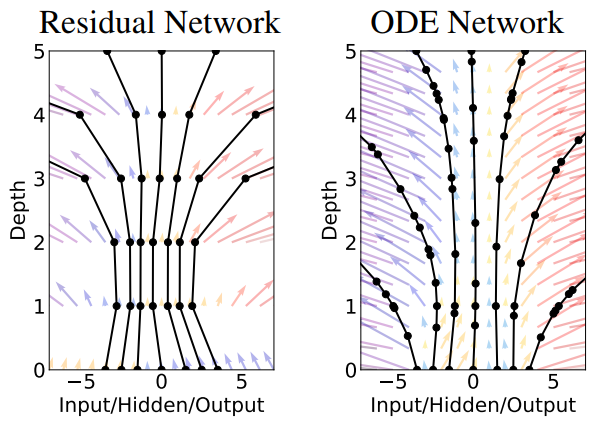
Trong phần 4.2, ta đã chia khoảng vi phân thành nhiều điểm rời rạc cách nhau $\delta_t$ để tính xấp xỉ bằng phương pháp Euler thuận. Trong trường hợp tổng quát, nếu $\delta_t$ tiến tới 0, số điểm chia là vô hạn và ta thu được một mạng phần dư vô hạn lớp tương đương. Khi đó ta thu được hàm $h(t)$ biến đổi liên tục trên miền $[t_0, t_N]$ chuyển dần $x$ thành $y$.
4.4. Mạng nơ-ron vi phân thường trong dự đoán chuỗi thời gian
Hàm $h(t)$ trong công thức (1) không chỉ dùng để biểu diễn mạng nhiều tầng, mà còn có thể sử dụng để biểu diễn trạng thái ẩn nói chung trong các mô hình động. Trong bài toán dự đoán chuỗi thời gian, dữ liệu vào là một chuỗi giá trị $x_1, x_2, …, x_N$ đến từ các thời điểm rời rạc $t_1, t_2, …, t_N$, chẳng hạn như tỉ giá ngoại tệ hàng ngày. Chuỗi thời gian có thể mô hình hóa bằng một mạng hồi quy RNN. Tuy nhiên, nhược điểm của mạng RNN thông thường là nó giả định trạng thái ẩn giữa hai bước liên tiếp nhau $t_{i-1}$ và $t_{i}$ là hằng số $h(t) = h_{t_{i-1}}, \forall t_{i-1} \le t < t_i$. Điều này rất tệ khi các thời điểm $t_i$ cách xa nhau hoặc được lấy mẫu không đồng đều (irregularly sampled data). Mạng hồi quy suy giảm RNN-Decay biểu diễn trạng thái ẩn giảm dần lũy thừa theo thời gian, giả thiết này cũng không thật sự phù hợp trong thực tế.
Mạng phương trình vi phần thường cho phép mô hình hóa đại lượng $x$ thông qua trạng thái ẩn trung gian $h(t)$ biến đổi liên tục theo $t$: $x_t \sim p(x|h(t), \theta_h)$. Mạng $h(t)$ được huấn luyện bằng phương pháp tự mã hóa biến phân (Variational Autoencoder) [7]. Sau khi học xong, ta có thể dùng $h(t)$ để ngoại suy các điểm dữ liệu $x_t$ trong tương lai ($t > t_N$) hoặc trong quá khứ ($t < t_1$), hoặc nội suy các điểm dữ liệu trung gian ($t_1 <t < t_N$).
Người viết: SangDV
5. Tài liệu tham khảo
1. Guido F. Montúfar, Razvan Pascanu, KyungHyun Cho, Yoshua Bengio. On the Number of Linear Regions of Deep Neural Networks. NIPS 2014: 2924-2932
2. Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun. Identity Mappings in Deep Residual Networks. ECCV (4) 2016: 630-645
3. Gao Huang, Zhuang Liu, Laurens van der Maaten, Kilian Q. Weinberger. Densely Connected Convolutional Networks. CVPR 2017: 2261-2269
4. Olaf Ronneberger, Philipp Fischer, Thomas Brox. U-Net: Convolutional Networks for Biomedical Image Segmentation. MICCAI (3) 2015: 234-241
5. Christoph Feichtenhofer, Axel Pinz, Richard P. Wildes. Spatiotemporal Multiplier Networks for Video Action Recognition. CVPR 2017: 7445-7454
6. Andreas Veit, Michael J. Wilber, Serge J. Belongie. Residual Networks Behave Like Ensembles of Relatively Shallow Networks. NIPS 2016: 550-558
7. Tian Qi Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud. Neural Ordinary Differential Equations. NeurIPS 2018: 6572-6583
8. Yulia Rubanova, Ricky T. Q. Chen, David Duvenaud. Latent ODEs for Irregularly-Sampled Time Series. CoRR abs/1907.03907 (2019)

