Contents
Bí ẩn đằng sau giải thuật SGD – Chính quy hóa ngầm
1. Chính quy hóa ngầm với giải thuật GD (Gradient Descent)
Định lý 1: Thuật toán GD không tối ưu trực tiếp hàm mục tiêu gốc $L(w)$ mà sẽ tối ưu hàm mục tiêu hiệu chỉnh khác:
$$\tilde{L}_{GD}(w) = L(w) + \frac{h}{4} ||\nabla L(w)||^2 \tag{2} \label{eq2}$$
trong đó đại lượng thứ 2 trong vế phải của Công thức (\ref{eq2}) gọi là chính quy hóa ngầm gradient [1].
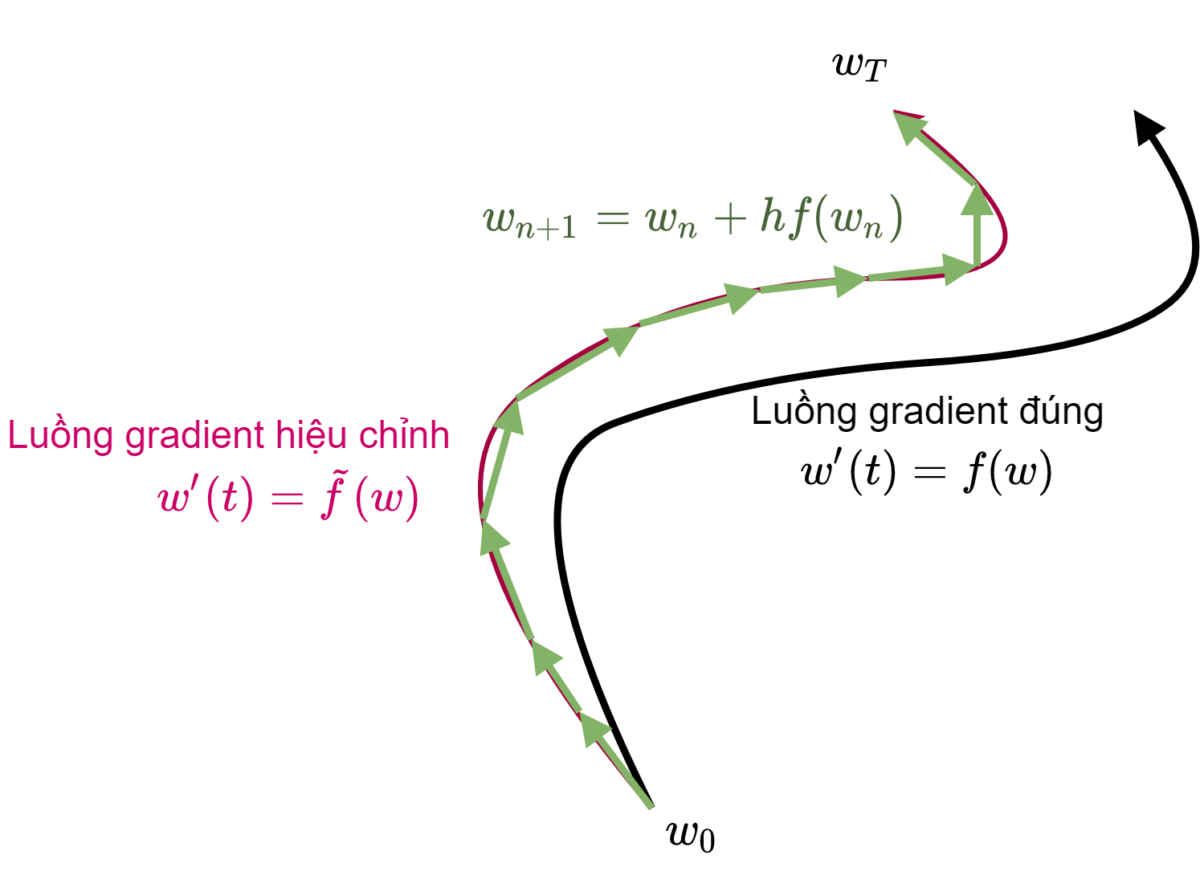
Phương pháp Euler thuận sinh ra nghiệm gần đúng $\{w_0, w_1, \ldots, w_n, …\}$ của phương trình vi phân ( $\ref{eqODE}$) với sai số cỡ $O(h^2)$ so với nghiệm chính xác. Do đó, đối với hàm mục tiêu gốc ban đầu $L(w)$ thì quỹ đạo tối ưu lý tưởng của véc-tơ tham số $w$ phải như đường màu đen trên Hình 1. Tuy nhiên thực tế giải thuật GD tối ưu tham số $w$ theo một quỹ đạo hoàn toàn khác (màu hồng trên Hình 1) và quỹ đạo này hướng tới tối ưu một hàm mục tiêu hiệu chỉnh $\tilde{L}(w)$ hoàn toàn khác.
Để đánh giá hàm mục tiêu hiệu chỉnh $\tilde{L}(w)$, người ta sử dụng phương pháp Phân tích lỗi ngược (Backward Error Analysis). Cụ thể, người ta thay đổi vế phải của phương trình ($\ref{eqODE}$) thành một hàm khác có dạng:
$$ \tilde{f}(w) = f(w) + hf_1(w) + O(h^2) \tag{5} \label{eqtildew}$$
trong đó $f_1(w)$ phải xác định sao cho dãy các điểm của nghiệm xấp xỉ $w_0, w_1, \ldots, w_n, …$ nằm chính xác trên nghiệm đúng của phương trình $w'(t) = \tilde{f}(w), w(0) = w_0$, nghĩa là:
$$w_n = \tilde{w}(t_n) = \tilde{w}(nh), \forall n = 0, 1, \ldots \tag{6} \label{eqConds} $$
Lưu ý theo quy tắc đạo hàm hợp ta có: $w^{”}(t) = \frac{dw'(t)}{dt} = \frac{d\tilde{f}(w)}{dt} = \frac{d\tilde{f}(w)}{dw}\frac{dw}{dt} = \nabla\tilde{f}(w)\tilde{f}(w)$.
Áp dụng khai triển Taylor cho $\tilde{w}(t+h)$ xung quanh $t$, ta có:
\begin{array}{lcl} \tilde{w}(t+h) &=& \tilde{w}(t) + h\tilde{w}'(t) + \frac{1}{2}h^2w^{”}(t) + O(h^3) \\ &=& \tilde{w}(t) + h\tilde{f}(w) + \frac{1}{2}h^2\nabla\tilde{f}(w)\tilde{f}(w) + O(h^3) \tag{7} \label{eq7} \end{array}
Thế Công thức (\ref{eqtildew}) vào (\ref{eq7}) ta có:
\begin{array}{lcl} \tilde{w}(t+h) &=& \tilde{w}(t) + h( f(w) + hf_1(w) + \ldots) + \frac{1}{2}h^2\left(\nabla f(w) + h\nabla f_1(w) + \ldots\right)\left(f(w) + hf_1(w) + \ldots\right) \\ &=& \tilde{w}(t) + hf(w) + \frac{1}{2}h^2\left(2f_1(w) + \nabla f(w) f(w)\right) + O(h^3) \tag{8} \label{eq8} \end{array}
Từ (\ref{eqEuler}) và (\ref{eqConds}) ta có:
$$ \tilde{w}(t_n+h) = w_{n+1} = w_n + hf(w) = \tilde{w}(t_n) + hf(w), \forall n = 0, 1, \ldots \tag{9} \label{eq9}$$
Để PT (\ref{eq9}) đúng với mọi $n$, thì các hệ số từ $h^2$ trở lên của vế phải PT (\ref{eq8}) phải đồng nhất với 0. Xét riêng hệ số của $h^2$ bằng 0, ta có:
$$f_1(w) = -\frac{\nabla f(w) f(w)}{2} = -\frac{1}{4} \nabla ||f(w)||^2$$.
Nếu $f(w) = -\nabla L(w)$, ta có: $f_1(w) = -\frac{1}{4}\nabla ||\nabla L(w)||^2$.
Do đó phương trình vi phân sau khi phân tích lỗi ngược của phương pháp Euler thuận trở thành:
$$ w'(t) = \tilde{f}(w) = – \nabla \left( L(w) + \frac{h}{4} ||\nabla L(w)||^2\right) + O(h^2)$$
và đây là luồng gradient của hàm mục tiêu hiệu chỉnh mới như ở Công thức (\ref{eq2}) nói trên.
Như vậy, giải thuật GD tự bản thân nó đã có hiệu ứng chính quy hóa ngầm để hạn chế hiện tượng học quá khớp. Cụ thể, hàm mục tiêu hiệu chỉnh $\tilde{L}_{GD}(w)$ trong Công thức (\ref{eq2}) phạt nặng đối với những vùng nhọn và dốc khi tại đó giá trị gradient của hàm mục tiêu $||\nabla L(w)||$ rất lớn.
2. Chính quy hóa ngầm với giải thuật SGD
Đối với trường hợp mini-batch SGD (sau đây gọi chung là giải thuật SGD), mọi thứ trở nên phức tạp hơn do dữ liệu bị hoán đổi vị trí (shuffle) trong mỗi epoch một cách ngẫu nhiên, dẫn tới quỹ đạo luồng gradient hiệu chỉnh cũng ngẫu nhiên chứ không tất định như trên Hình 1. Như vậy xuất phát từ giá trị khởi tạo $w_0$ sẽ có tồn tại nhiều quỹ đạo luồng gradient hiệu chỉnh khác nhau tạo thành một phân phối. Mục tiêu của nghiên cứu trong [2] là sử dụng kỹ thuật phân tích lỗi ngược để ước lượng quỹ đạo hiệu chỉnh kỳ vọng của phân phối này.
Định lý 2: Giả sử tập huấn luyện có $N$ mẫu được chia đều thành $m = N/B$ lô bằng nhau với kích thước $B$ mẫu mỗi lô; $\hat{L}_k(w)$ là hàm chi phí tính trên lô dữ liệu (batch) thứ $k$ với $k = 1, \ldots, m$. Giả sử các lô dữ liệu là cố định và ta chỉ hoán vị ngẫu nhiên thứ tự các lô khi huấn luyện. Khi đó sau một epoch, thuật toán SGD hiệu chỉnh hàm mục tiêu $L(w)$ thành một hàm khác có kỳ vọng được tính trên tất cả các phương án hoán vị lô dữ liệu bằng:
\begin{array}{lcl} \tilde{L}_{SGD}(w) &=& L(w) + \frac{h}{4m} \sum\limits_{k=1}^{m}||\nabla \hat{L}_k(w)||^2 \\ &=& L(w) + \frac{h}{4} ||\nabla L(w)||^2 + \frac{h}{4m} \sum\limits_{k=1}^{m}||\nabla \hat{L}_k(w) – \nabla L(w)||^2 \\&=& \tilde{L}_{GD}(w) + \frac{h}{4m} \sum\limits_{k=1}^{m}||\nabla \hat{L}_k(w) – \nabla L(w)||^2 \tag{10} \label{eq10} \end{array}
Chứng minh chi tiết Định lý 2 có thể tham khảo trong [2]. Về cơ bản, chứng minh này là mở rộng từ ý tưởng chứng minh Định lý 1, trong đó cập nhật Euler thuận được thực hiện $m$ lần liên tiếp qua $m$ lô dữ liệu (thay vì cập nhật một lần như đối với GD).
Có thể thấy, hàm mục tiêu hiệu chỉnh $\tilde{L}_{SGD}(w)$ trong Công thức (\ref{eq10}) không chỉ phạt nặng đối với những vùng nhọn và dốc khi tại đó giá trị $||\nabla L(w)||$ rất lớn, mà còn phạt nặng những phần không đồng đều (non-uniform) có phương sai cao giữa các lô dữ liệu $\sum\limits_{k=1}^{m}||\nabla \hat{L}_k(w) – \nabla L(w)||$. Một cách trực quan, nếu phương sai hàm mục tiêu giữa các lô dữ liệu là thấp, nghĩa là tại vùng đó hàm mục tiêu ổn định hơn, dù nhận lô dữ liệu nào thì cũng cho độ chính xác tương đồng nhau. Điều này gợi ý cho chúng ta suy nghĩ rằng, tại ví trí đó mô hình sẽ hoạt động ổn định bất kể dữ liệu tới từ tập huấn luyện hay tập kiểm thử, tức là có khả năng tổng quát hóa tốt.
Vì vậy bản chất giải thuật SGD tự ngầm định sẽ thiên vị những vùng rộng và phẳng hơn trên bề mặt hàm mục tiêu và tại đó mô hình huấn luyện được sẽ có xu hướng hoạt động ổn định hơn và có khả năng tổng quát hóa tốt.
Một lưu ý quan trọng, hàm mục tiêu hiệu chỉnh $\tilde{L}_{GD}(w)$ của giải thuật GD và hàm mục tiêu gốc $L(w)$ có cùng chung cực tiểu toàn cục (do tại cực tiểu toàn cục ta có $||\nabla L(w)|| = 0$). Tuy nhiên cực tiểu toàn cục của $L(w)$ không nhất thiết là cực tiểu toàn cục (thậm chí không phải là cực tiểu địa phương) của hàm hiệu chỉnh $\tilde{L}_{SGD}(w)$. Nếu mạng nơ-ron bị tham số hóa quá mức vượt ngưỡng nội suy (interpolation threshold), thì sai số trên tất cả các lô dữ liệu bằng 0, và khi đó cực tiểu toàn cục của hai hàm $\tilde{L}_{SGD}(w)$ và $L(w)$ sẽ trùng nhau.
Định lý 2 giả định các lô dữ liệu là cố định và ta chỉ ước lượng hàm mục tiêu hiệu chỉnh kỳ vọng trên tập các hoán vị của các lô dữ liệu này sau một epoch. Với giả định này ta đã chỉ ra rằng có sự chính quy hóa gradient ngầm trong thuật toán SGD. Tuy nhiên, huấn luyện mạng nơ-ron thường đòi hỏi tiến hành qua nhiều epoch, và mỗi epoch chứa các lô dữ liệu khác nhau. Do đó để đánh giá chính xác hơn sự chính quy hóa ngầm này trong quá trình huấn luyện thực tế, ta cần ước lượng hàm mục tiêu hiệu chỉnh kỳ vọng trên toàn bộ các hoán vị của tập huấn luyện.
Định lý 3: Giả sử tập huấn luyện có $N$ mẫu được chia đều thành $m = N/B$ lô bằng nhau với kích thước $B$ mẫu mỗi lô; $L_i(w)$ là hàm mất mát tính trên dữ liệu thứ $i$ với $i = 1, \ldots, N$. Khi đó sau mỗi epoch, thuật toán SGD hiệu chỉnh hàm mục tiêu $L(w)$ thành một hàm khác là $\tilde{L}_{SGD}(w)$ có kỳ vọng được tính trên tất cả các hoán vị tập huấn luyện bằng:
$$ \mathbb{E} [\tilde{L}_{SGD}(w)] = L(w) + \frac{h}{4} ||\nabla L(w)||^2 + \frac{N-B}{N(N-1)} \frac{h}{4B} \sum\limits_{k=1}^{m}||\nabla L_i(w) – \nabla L(w)||^2 \tag{11} \label{eq11} $$
3. Vài trò của tốc độ học và kích thước lô đối với khả năng tổng quát hóa
Từ Công thức (\ref{eq11}), ta có thể thấy hệ số phạt của đại lượng chính quy hóa thứ hai tỉ lệ thuận với tốc độ học và tỉ lệ nghịch với kích thước lô dữ liệu. Do đó, tốc độ học càng lớn hoặc kích thước lô càng nhỏ thì hệ số phạt càng lớn và có thể cải thiện khả năng tổng quát hóa, giúp mô hình chống hiện tượng học quá khớp.
Để chứng minh điều này, tác giả trong [2] đã đưa đại lượng chính quy hóa ngầm của SGD vào trực tiếp trong hàm mục tiêu để huấn luyện với hệ số điều khiển $\lambda$:
$$L(w) + \frac{\lambda}{4m}\sum\limits_{k=1}^{m}||\nabla \hat{L}_k(w)||^2 \leftarrow \min$$
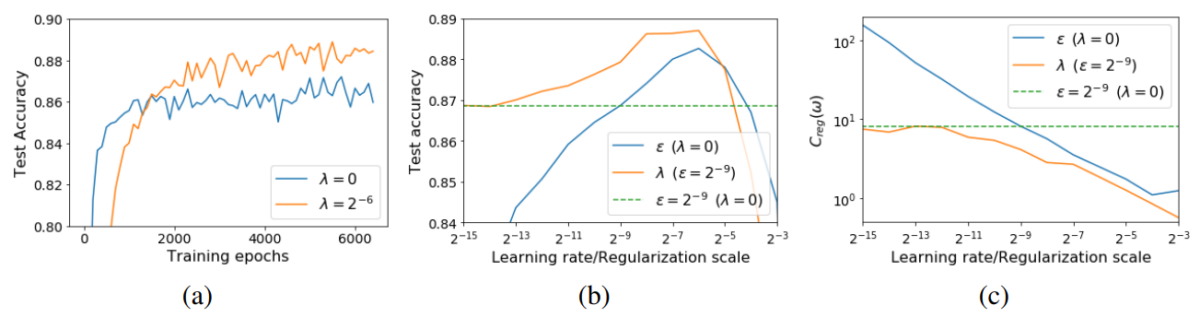
Hình 2 cho thấy sự ảnh hưởng của tốc độ học tới khả năng tổng quát hóa của mô hình WideResNet-10 huấn luyện trên tập CIFAR10. Chú ý, ở trên Hình 2 ký hiệu tốc độ học là $\epsilon$ nhưng trong bài blog này ta ký hiệu là $h$. Từ Hình 2 nhận thấy rằng, khi tăng dần tốc độ học thì độ chính xác trên tập kiểm thử sẽ tăng dần. Đến một ngưỡng nào đó (ở đây là $h_{opt} = 2^{-6}$, nếu tăng tiếp thì độ chính xác trên tập kiểm thử sẽ giảm do hiện tượng dưới khớp (underfitting) xảy ra. Điều này cũng diễn ra tương tự khi ta phạt hàm mục tiêu một cách tường minh bằng cách thay đổi hệ số điều khiển $\lambda$.
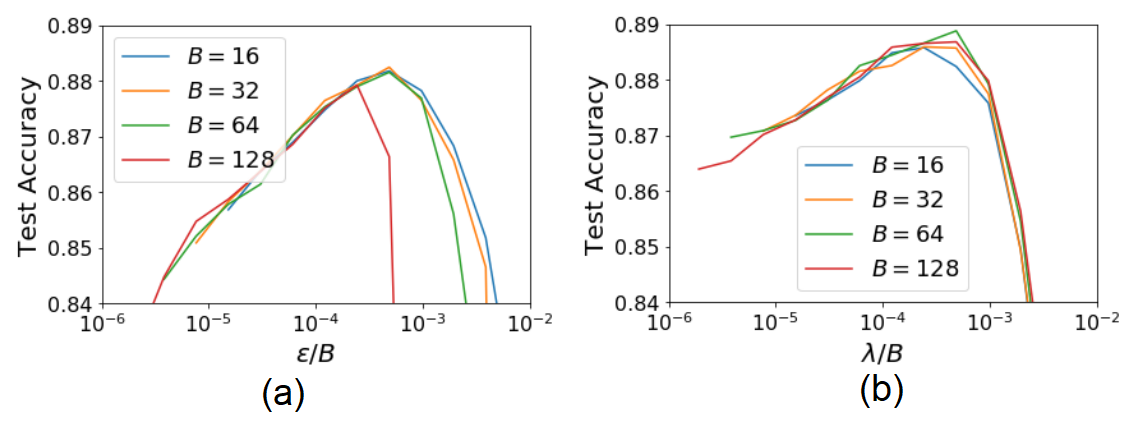
Hình 3 nghiên cứu sự ảnh hưởng của kích thước lô tới khả năng tổng quát hóa. Ta thấy rằng, khi tỉ lệ giữa tốc độ học và kích thước lô được giữ ổn định và kích thước lô không quá lớn thì độ chính xác trên tập kiểm thử gần như ngang nhau đối với các kích thước lô khác nhau. Nhưng nếu kích thước lô quá lớn thì điều này không còn đúng nữa (ví dụ với $B=128$ trên Hình 3a). Khi kích thước lô quá lớn thì đại lượng chính quy hóa thứ nhất trong Công thức (\ref{eq11}) lấn át đại lượng chính quy hóa thứ 2. Khi đó giải thuật SGD sẽ có hành vi tương tự với giải thuật GD. Tác giả cho rằng, tại giới hạn này, giá trị tốc độ học hoàn toàn độc lập với kích thước lô.
4. Một góc nhìn khác về giải thuật SGD
Trong trường hợp mạng tuyến tính sử dụng các hàm mất mát khác nhau, người ta đã chứng minh được rằng giải thuật SGD sẽ hội tụ tới lời giải với chuẩn $\mathcal{l}2$ nhỏ nhất (minimum norm solution) [3]. Lời giải với chuẩn nhỏ nhất sẽ cực đại hóa lề phân tách (tương tự như trong SVM), và điều này giúp cho mô hình có khả năng tổng quát hóa tốt.
Đối với trường hợp tổng quát, tác giả trong [4] chỉ rằng tại vùng lân cận cực tiểu phẳng toàn cục của hàm mục tiêu, mạng nơ-ron hoạt động tương tự các mô hình tuyến tính và vì vậy kế thừa rất nhiều tính chất của mô hình tuyến tính.
SGD có sự liên quan gì với Neural ODE [5]? Có thể hiểu giải thuật SGD sử dụng phương pháp Euler thuận để giải phương trình vi phân ODE: $w'(t) = – \nabla L(w)$ với $t$ thể hiện số thứ tự của bước lặp, bắt đầu từ tham số khởi tạo $w_0$ tại thời điểm $t=0$, kết thúc là tham số tối ưu $w_T$ tai thời điểm $t=T$, với $T$ là số bước lặp. Neural ODE sử dụng phương pháp Euler thuận để giải phương trình vi phân ODE đối với mô hình $h(t)$, với $t$ là số thứ tự lớp của mạng nơ-ron, bắt đầu từ dữ liệu vào $x$ tại thời điểm $t=0$, kết thúc bởi đầu ra $y$ tương ứng tại thời điểm $t=n$, với $n$ là số lớp của mạng.
5. Kết luận
Giải thuật SGD và GD có hiệu ứng chính quy hóa gradient ngầm. Giải thuật SGD tự biết cách né tránh các hố cực tiểu nhọn hoặc nhấp nhô để tìm tới các vùng phẳng và đồng đều trên bề mặt hàm mục tiêu, nơi thường có khả năng tổng quát hóa cao. Hiệu ứng chính quy hóa ngầm của SGD phụ thuộc tỉ lệ thuận với tốc độ học và tỉ lệ nghịch với kích thước lô dữ liệu. Khi kích thước lô dữ liệu quá lớn vượt một ngưỡng nào đó, giải thuật SGD sẽ mất dần khả năng tránh các vùng nhấp nhô (non-uniform) và hoạt động tương tự với giải thuật GD.
Người viết: SangDV
6. Tài liệu tham khảo
1. David G. T. Barrett, Benoit Dherin: Implicit Gradient Regularization. ICLR 2021
2. Samuel L. Smith, Benoit Dherin, David G. T. Barrett, Soham De: On the Origin of Implicit Regularization in Stochastic Gradient Descent. ICLR 2021
3. Ashia C. Wilson, Rebecca Roelofs, Mitchell Stern, Nati Srebro, Benjamin Recht: The Marginal Value of Adaptive Gradient Methods in Machine Learning. NIPS 2017: 4148-4158
4. Tomaso A. Poggio, Kenji Kawaguchi, Qianli Liao, Brando Miranda, Lorenzo Rosasco, Xavier Boix, Jack Hidary, Hrushikesh Mhaskar: Theory of Deep Learning III: explaining the non-overfitting puzzle. CoRR abs/1801.00173 (2018)
5. Tian Qi Chen, Yulia Rubanova, Jesse Bettencourt, David Duvenaud. Neural Ordinary Differential Equations. NeurIPS 2018: 6572-6583

